12 klocków
W rzędzie leży 12 ponumerowanych sześciennych klocków w trzech kolorach – 4 różowe, 4 żółte i 4 niebieskie (górny rysunek).
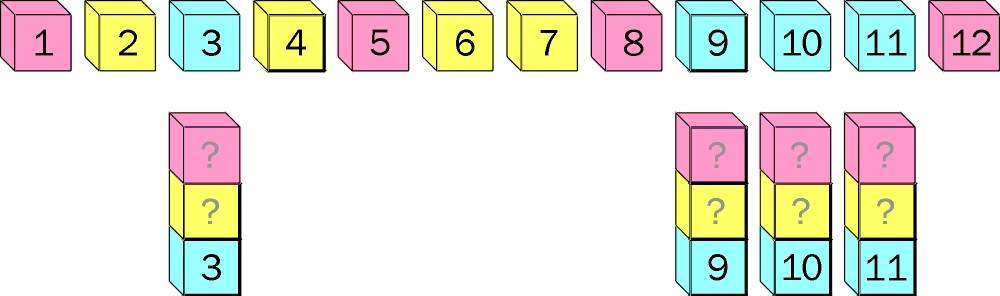
Zadanie polega na przekształceniu tego układu w cztery jednakowe 3-klockowe wieże (dolny rysunek). Trzeba to zrobić w ośmiu ruchach, a każdy ruch polega na przeskoczeniu klockiem w rzędzie w sumie przez 3 klocki (uwzględniając pojedyncze oraz tworzące 2- i 3-klockowe wieże) i umieszczeniu „skoczka” na czwartym klocku – pojedynczym lub wieńczącym 2-klockową wieżę.
Rozwiązaniem może być zapis skoków albo oznaczenie odpowiednimi numerami różowych i żółtych klocków w wieżach.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Śliskie te zasady trochę, mam nadzieję, że dobrze zrozumiałem.
Wyszło mi tak:
7 na 3
8 na 7
4 na 10
6 na 11
5 na 6
12 na 4
2 na 9
1 na 2
Jest super! (tylko w końcowym tercecie może być inna kolejność).
mp
Czy jeden pojedynczy klocek plus jeden podwójny klocek to dwa klocki czy trzy klocki?
Nie ma pojęcia „podwójny klocek”. Jest wieża 2- lub 3-klockowa, czyli wieża z 2 klocków to 2 klocki, więc przeskakuje się przez 2 klocki. Analogicznie jest z wieżą 3-klockową – wystarczy przez nią hycnąć, aby zaliczyć 3 klocki.
mp
Wartości odczytywane poziomo od lewej:
poziom trzeci / łososiowy:
8,1,12,5
poziom drugi / żółty:
7,2,4,6
poziom pierwszy / zielonkawy:
3,9,10,11 🙂
Łamigłówka jest ciekawa dla różnych metod rozwiązywania.
Metoda „reverse engineering”/”od końca” napotykała problemy.
Kolejne przestawienia w rozwiązaniu:
7 => 3
8 => 3
4 => 10
6 => 11
5 => 11
Ostatnie trzy przestawienia (warianty):
2 => 9
1 => 9
12 => 10
albo
2 => 9
12 => 10
1 => 9
albo
12 => 10
2 => 9
1 => 9
8/7/3, 1/2/9, 12/4/10, 5/6/11
Wieże:
8 1 12 5
7 2 4 6
3 9 10 11
Kolejne ruchy:
7, 8, 4, 6, 5, 2, 1, 12 (ruch 12 można wykonać przed 1 lub przed 2)
Zadanie wydaje się łatwe, ale tak nie jest. Na razie wyłgam się żartem i aby zwiększyć swoje szanse, zsuwam wszystkie klocki razem.
Wykonuję sześć skoków: 1) 6/10, 2) 4/9, 3) 12/4, 4) 7/11, 5) 5/7, 6) 8/6.
Otrzymuję cztery 3-klockowe zestawy: 1-2-3, 12-4-9, 8-6-10, 5-7-11.
Jeżeli koniecznie musi być osiem ruchów, można dodać dwa:
7) stawiamy 1-2-3, 8) przewracamy 5-7-11.
8, 1,12, 5
7, 2, 4, 6
3, 9,10,11
Spóźniwszy się z rozwiązaniem mogę tylko dorzucić, że jest 8 sposobów dojścia do jedynego rozwiązania.
@Spytko z Melsztyna
W moim rozwiązaniu pięć pierwszych posunięć jest stałe.
Wypisałem 3 możliwe warianty zakończenia zabawy.
To samo wynika z komentarza @grgkh.
Jak doliczyć się tych 8 możliwości ?
@apartado
Faktycznie są tylko 3 warianty. Tak to jest gdy się robi coś późno 🙂
https://zapodaj.net/plik-JU816j9fnx