Dominik
Są miasta-imiona (np. Kazimierz, Jarosław, Marki, Mikołajki, Sława), rośliny-imiona (róża, narcyz, dalia, hiacynt, hortensja, marek i jeszcze parę), a nawet zwierzęta-imiona (np. ryś, jerzyk, alka, tobiasz). A łamigłówek imion sobie nie przypominam – chyba że uznamy za łamigłówkę krzyżówkę zwaną jolką. Aby nadrobić ten nikomu niepotrzebny brak wymyśliłem dominika. Z imienia łatwo wywnioskować, że ma on związek z moim ulubionym łamigłówkowym rekwizytem, czyli dominem.
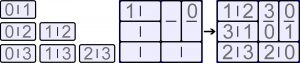
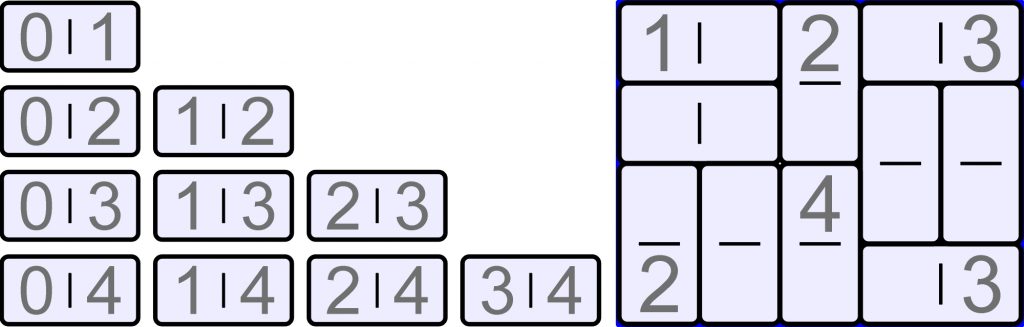
Z dziesięciu dominowych kamieni, tworzących tzw. komplet czwórkowy bez dubletów, należy ułożyć prostokąt 4×5 zgodnie z podanym schematem (rysunek), ale tak, by nie stykały się ze sobą:
– połówki kamieni z taką samą liczbą;
– kamienie z taką samą różnicą liczb umieszczonych na połówkach (różnice wynoszą od 1 do 4).
Kilka liczb zostało już ujawnionych na właściwych miejscach.
W przykładzie kamieni jest sześć (komplet trójkowy bez dubletów), więc mniejszy jest także prostokąt (3×4) i zakres różnic (od 1 do 3).
Przykład:
Zadanie jest małe, ale nieco twardawe i podstępne. W związku z tym pytanie: ile ma rozwiązań?
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Rozwiązania są co najmniej cztery. Ale, gdybyśmy wstawili do diagramu, na przykład jedynkę pod górną trójką, to odpowiedź byłaby jedna:
10203
41041
32402
24313
Są cztery rozwiązania, dwa istotnie różne oraz dwa duale. Tak myślę…
Szturmem trudne do zdobycia, ale sprytnym sposobem w 20 min.
https://images89.fotosik.pl/644/698e697a097b6bbb.jpg
są tylko 2 rozwiązania:
10243
41032
13404
21023
10243
41034
13402
21023
Bardzo ciekawe zadanie, najważniejsze to znaleźć punkt zaczepienia. Ja sobie wybrałem prawy górny róg. Może być tam (0,3), (1,3), (4,3). Przy (1,3) nie da się nic zrobić. Przy (4,3) dochodzimy do:
10243
4103x
1340y
21023
(x,y) to (2,4) – można go ułożyć na 2 sposoby.
Przy (0,3) dochodzimy do:
10203
4104x
3240y
24313
Znów jest (x,y), tym razem jako (1,2), i można tak, albo tak.
Są cztery rozwiązania:
1
1 0 2 0 3
4 1 0 4 1
3 2 4 0 2
2 4 3 1 3
——————
2
1 0 2 0 3
4 1 0 4 2
3 2 4 0 1
2 4 3 1 3
——————
3
1 0 2 4 3
4 1 0 3 2
1 3 4 0 4
2 1 0 2 3
——————
4
1 0 2 4 3
4 1 0 3 4
1 3 4 0 2
2 1 0 2 3
——————
1 i 2 oraz 3 i 4 różnią się tylko obróconym jednym kamieniem.
Przy ręcznej robocie to rzeczywiście dłubanina ale program liczy w sekundę.