Siódemkowo
Jeśli siódemka jest liczbą szczęśliwą, to rok 2023 można by uznać – ze względów arytmetycznych – także za szczęśliwy (w realu niewiele na to wskazuje). Główne względy są trzy. Po pierwsze: suma cyfr tegorocznej liczby równa się 7; po drugie: liczba ta dzieli się przez 7; po trzecie: w jej rozkładzie na czynniki pierwsze siódemki dominują: 2023=7×17×17. W związku z tym rozkładem 2023 należy do tzw. liczb Einsteina, ponieważ stanowi „bliźniaczkę” słynnego wzoru E=mc2 – jest w tym wzorze energią, 7 to masa, a 17 – szybkość światła. Jest jeszcze czwarty wzgląd, nawet bardziej spektakularny, ale innego rodzaju: 2023 zalicza się do liczb zwanych szczęśliwymi. Liczby te zostają oddzielone od „plew” w wyniku przesiewania ciągu liczb naturalnych przez sito Flawiusza, działające podobnie do sita Eratostenesa: na początku odpada każda co druga liczba, a w każdym kolejnym kroku każda co n-ta, gdzie n jest najmniejszą liczbą pozostałą po odsiewie w poprzednim kroku, ale większą niż n-1 (trochę to zawiłe, więc dla rozjaśnienia odsyłam do Wikipedii).
W poszukiwaniu innych osobliwości 2023 przejrzałem kilka liczbowych panoptików, ale równie efektownych, a niezbyt wyszukanych, nie znalazłem. Warto tylko wspomnieć o jednej wyszukanej albo lepiej zilustrować ją przykładem: 2023=(2+0+2+3)×(22+02+22+32)2. Ciekawe, że liczb o takiej własności jest (jakże by inaczej) tylko siedem.
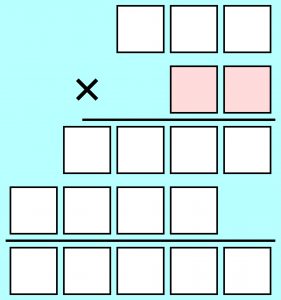
W poniższym zapisie mnożenia cyfry zastąpiono kratkami. Większość z nich należy do zbioru {0, 2, 3, 7}. Inne są tylko ukryte za różowymi kratkami dwie cyfry tworzące mnożnik. Czy rozszyfrowanie mnożenia jest łatwe?
Na koniec początku (roku) warto zauważyć, że rok 2023 jest czwartym w XXI wieku „urodzonym” w niedzielę. Następny taki rok-obibok przyjdzie na świat za 11 lat.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Metodą prób i błędów dość szybko znalazłem 223 x 99 = 22077, program później znalazł róznież 230 x 99 = 22770.
Szczęśliwego Nowego Roku 2023!
230×99=22770, 223×99=22077.
Wszystkiego najlepszego w nowym roku.
Już jutro wydarzy się cud!
Mam rozwiązanie, poprawne chociaż mało satysfakcjonujące.
2 2 3 x 9 9 ------------ 2 0 0 7 2 0 0 7 ------------ 2 2 0 7 7Znalezienie tego było łatwe, nie jestem pewna czy są inne, ale ich nie wykluczam.
223*99 = 22077. W środkowych kratkach 223*9 = 2007. Jeśli miałoby to świadczyć o jakimś szczególnym powinowactwie roku 2023 z 2007, to próbowałem sobie przypomnieć, co wydarzyło się w 2007 roku, no więc ówczesna partia rządząca w Polsce oddała władzę w wyniku wyborów, to chyba najważniejsze wydarzenie krajowe. Poza tym Adam Małysz zdobył swój ostatni puchar świata, a piłkarze po raz pierwszy zakwalifikowali się na Euro w roku następnym, czyli 2008, pod wodzą Leo Beenhakkera. No ale to już historia, a na rok 2023 najlepsze życzenia, przede wszystkim zdrowia.
Jest jeszcze 7^7 mod 7! = 2023
O szczęściu:
Przez przypadek dowiedziałem się, że 2023 w zapisie szestnastkowym ma dominującą obecność siódemek.
Nie przez przypadek dowiedziałem się, że cyfra 7 występuje (pierwsze pojawienie się) w rozwinięciu dziesiętnym liczby Pi na miejscu 13.
Mnożników 3-cyfrowych jest 48, najpierw mnożymy tę liczbę przez drugą cyfrę różowego mnożnika {1,4,5,6,8,9} tak by iloczyn był 4-cyfrowy i z naszego zbioru. stąd wynika że szukane cyfry to tylko 6 i 9 dla 9ciu mnożników 3-cyfrowych. Następnie wystarczy sparawdzić kombinacje 66,69,96 i 99 na obu etapach mnożenia i tylko iloczyny 99 i 223 lub 99 i 230 spełniają warunki, stąd łatwo jest określić mnożnik.
Jeśli można proszę skasować mój poprzedni komentarz, skopiowałam tylko pierwszą część mnożenia stąd cały nie ma sensu.
223 x 99 = 2007 + 20070 = 22077
230 x 99 = 2070 + 20700 = 22770
Rozwiązania są 2:
223 * 99 = 2007 + 2007 = 22077
230 * 99 = 2070 + 2070 = 22770
Mnożenie zajęło mi nieznośnie dużo czasu – aż do momentu, kiedy zorientowałem się, że 0 może być na końcu… Jak widać forma nowroczna się dała we znaki 🙂
230 x 99 = 22770
Na logikę nic nie wskórałem, więc zacząłem przeczesywać liczby trzycyfrowe po kolei. Długo nie czekałem, bo już 223 i chwilę potem 230 dały czterocyfrowe iloczyny z 99, ale dalej już nic (o ile czegoś nie przegapiłem)…
Ciekaw jestem, czy istnieje rozwiązanie czysto dedukcyjne, cyfra po cyfrze.
Liczba 3-cyfrowa (mnożna) może zaczynać się na 2,3,7 (200-777)
Bardziej szczegółowo
200-277, 300-377, 700-777
Jeszcze bardziej szczegółowo pierwszy zakres (pozostałe podobnie)
200,202,203,207,220,222,223,227,230,232,233,237,270,272,273,277
Liczba 4-cyfrowa z grubsza
2000-2777, 3000-3777, 7000-7777
7AB = 700 + AB
7AB * 9 = 6300 + 9 * AB = 6300 + 9 * 77 = 6300 + 693 = 6993 < 7000 … (nie)
7AB * 8 = 5600 + 8 * AB = 5600 + 8 * 77 = 5600 + 616 = 6216 < 7000 … (nie)
7AB * 6 = 4200 + 6 * AB … (nie)
7AB * 5 = 3500 + 5 * AB (40-77 = 70,72,73,77) = 3850 + 5 * B (2,3,7) … (nie)
7AB * 4 = 2800 + 4 * AB (50-77 = 70,72,73,77) = 3000 + 4 * B (2,3,7) … (nie)
3AB = 300 +AB
3AB * 9 = 2700 + 9 * AB (00,02,03,07,20,22,23,27,30,32,33,37,70,72,73,77)
3AB * 9 = 2700 + 9 * AB (00,03,37,70) = 2700; 2727; 3033; 3330 … (tak)
3AB * 8 = 2400 + 8 * AB (02,03,07,20,22,23,27,30,32,33,37,70,72,73,77) … (nie)
3AB * 6 = 1800 + 6 * AB (02,03,07,20,22,23,27,30,32,33,37,70,72,73,77)
3AB * 6 = 1800 + 6 * AB (37,70,72) = 2022; 2220; 2232 … (tak)
3AB * 5 = 1500 + 5 * AB (02-77) … (nie)
3AB * 4 = 1200 + 4 * AB (02-77) … (nie)
2AB = 200 +AB
2AB * 9 = 1800 + 9 * AB (02,03,07,20,22,23,27,30,32,33,37,70,72,73,77)
2AB * 9 = 1800 + 9 * AB (23,30) = 2007; 2070 … (tak)
2AB * 8 = 1600 + 8 * AB (02,03,07,20,22,23,27,30,32,33,37,70,72,73,77) … nie
2AB * 6 = 1200 + 6 * AB (02,03,07,20,22,23,27,30,32,33,37,70,72,73,77) … nie
2AB * 5 = 1000 + 5 * AB (02,03,07,20,22,23,27,30,32,33,37,70,72,73,77) … nie
2AB * 4 = 800 + 5 * AB (02,03,07,20,22,23,27,30,32,33,37,70,72,73,77) … nie
Dziewięć liczb 4-cyfrowych jako bliźniaki jednojajowe, w tym cztery liczby jako bliźniaki dwujajowe, razem trzynaście sum do sprawdzenia i tylko jedno spełnienie.
230*99 = 2070 + 20700 = 22770
Sa DWA rozwiązania:
223 * 99 = 22077
230 * 99 = 22770