Kwadrat gamiczny

24 września 2022
Marek Penszko

Kwadrat magiczny n×n jaki jest, każdy widzi – na przykładzie dla n=4:

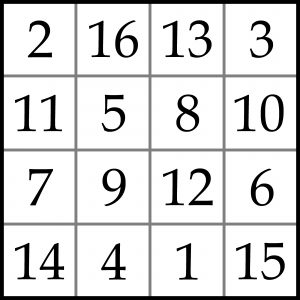
Do diagramu wpisane są kolejne liczby od 1 do n^2 w taki sposób, że suma n liczb w każdym wierszu, kolumnie i na obu głównych przekątnych jest taka sama – równa (n^3+n)/2.
Kwadrat gamiczny to kuzyn magicznego (stąd „czeskobłędna” nazwa), a przykład dla n=4 wygląda tak:

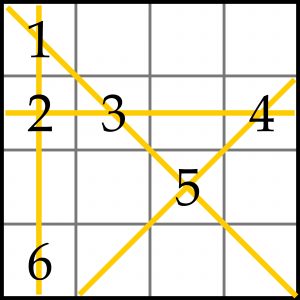
I definicja: do niektórych pól diagramu n×n wpisanych jest k kolejnych liczb – od 1 do k (k<<n^2; „<<” oznacza „znacznie mniejsze”) tak, że spełnione są dwa warunki:
– jeśli w jakimś wierszu, kolumnie lub na dowolnej przekątnej (głównej albo równoległej do niej) występują co najmniej dwie liczby, to ich suma jest zawsze jednakowa;
– k jest największą możliwą liczbą.
Poniżej znajduje się przykład kwadratu magicznego 5×5, a obok niego powinien pojawić się kwadrat gamiczny tego samego formatu. Jak mógłby wyglądać? – и от питання.

Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.