Pokój w Hetmanii
W marcowym Świecie Nauki było zadanie, które sprawiło rozwiązującym sporo kłopotu. A co istotniejsze, nierozstrzygniętym pozostała liczba rozwiązań. Może tutaj uda się to rozstrzygnąć.
Rzecz dzieje się w Hetmanii, czyli na szachownicy 9×9 zasiedlonej przez 9 hetmanów. Hetmany rozmieszczone są bezkonfliktowo – żaden nie atakuje swojego ziomka, a więc w każdym wierszu, kolumnie i na każdej linii ukośnej wyznaczonej przez przekątne pól stoi tylko jeden.
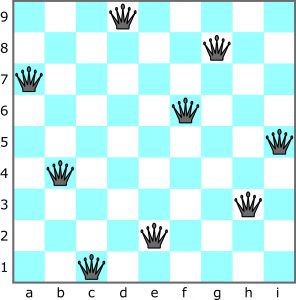
Zadanie polega na przesunięciu trzech z nich – zgodnie z zasadą poruszania się tych figur – tak, by zgoda została zachowana, czyli by żaden hetman nadal nie poczuł się bezpośrednio zagrożony. Powinien być jednak spełniony następujący warunek: łączny dystans trzech przesunięć powinien być jak najkrótszy.
Oto dwa przykłady trzech ruchów bezwarunkowych:
a7-a4, b4-b1, c1-c7 – dystans 12
d9-g6, f6-d8, g8-f9 – dystans 8,4
Łączne dystanse w obu przypadkach są wyraźnie za długie. Na pewno można krócej. A jak najkrócej?
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Jeśli w drugim przykładzie „łączny dystans trzech przesunięć ” wynosi 8,4 to poproszę o definicję tego pojęcia.
Dystans jest odległością między środkami pól (odległość między środkami sąsiednich pól w rzędzie lub kolumnie = 1). Łączny dystans jest sumą tych odległości. W drugim przykładzie suma ta równa jest sqrt18+sqrt8+sqrt2=8,4 (jeśli bliżej podłogi, choć lepszy byłby sufit, czyli 8,5).
mp
Chyba trochę prościej można opisać długość drogi w przypadku ruchów ukośnych:
W drugim przykładzie Hetmany zostały przesunięte ukośnie o 6 kroków, czyli droga ma długość 6 pierwiastków z 2.
Oczywiście 🙂
mp
Przykład:
d9-d8
f6-g6
g8-f9
Dystans: 1 + 1 + sqrt2 ~ 3,4
Krótszego dystansu (d = 1 + 1 + 1 = 3) osiągnąć się nie da i to bez względu na to jak ustawione są hetmany.
I wydaje się, że to jedyne rozwiązanie (?)
mp
Nie znam się zbytnio na szachach (może to jest problem) ale zastosowanie metryki kartezjańskiej wprowadza tu moim zdaniem element „nieszachowy”. Pojedynczy ruch Hetmana odbywa się wzdłuż linii prostej o k pól i to jest najprostsza i naturalna miara długości w szachach. Np. ruch d9-g6 ma długość 3 bo to ruch o 3 pola. Dla wieży oczywiście taki ruch składa się z dwu elementarnych więc ma długość 6. Metryka liniowa, nie dość że prostsza do liczenia, chyba bardziej odpowiada logice szachowej niż kartezjańska. Czy Hetman męczy się bardziej wykonując ruch na skos niż w pionie /poziomie albo taki ruch jest niżej oceniany? Widzę to tak: Hetman – nie, ale szachista owszem, choć różnica jest niewielka.
Powstaje ciekawe pytanie, czy rozwiązanie zadania (najkrótszy ruch) jest wrażliwe na taką zmianę przyjętej metryki?
@Markoniusz
Widzę to tak:
Mądrzejsi ode mnie ustalili takie właśnie zasady zagadki, więc zakładam, że mieli w tym swój uzasadniony powód.
Taki sposób liczenia długości drogi może być jakąś podpowiedzią.
Przejdźmy od słów do czynów:
Zalicytuję 3.41
Jeśli to zła odpowiedź , to nie zazdroszczę Gospodarzowi decyzji, czy już ją ujawnić 😉
Ruch o takiej samej długości wg obu metryk to
a7-c7; b4-a4; c1-b1
dist = 2+1+1 = 4 (translacje poziome)
Nie wydaje się możliwy ruch krótszy więc zaryzykuję tę odpowiedź.
Szanowny Autor już rozwiązanie podał, lepszego nie znajdę:
f6 –> g6 (1)
g8 –> f9 (√2)
d9 –> d8 (1)
Czyli 2+√2
Liczba rozwiązań istotnie różnych: 8
Nie uwzględniając symetrii: 64
Dla długości trasy 3.41
Proszę o podanie ośmiu istotnie różnych rozwiązań.
mp
a7-c7, b4-a4, c1-b1 – dystans 4
d9-d8, f6-g6, g8-f9 – dystans 3,4
2+2✓2=4,83
https://www.fotosik.pl/zdjecie/usun/x6Eo3k~VfX_K19tP3S295BXdrwL9OG
Proszę o informację, czy da się uzyskać mniej.
Tak, może być mniej
mp
https://www.fotosik.pl/zdjecie/usun/SBOe2iVdkFAUIVlws6ROmb_7bQE1DR
Odległość 3.41 wszystko tłumaczy 😉
Powinienem wysłać ten link:
https://www.fotosik.pl/zdjecie/e0fe752efeda9a2c
Poprzedni daje możliwość usunięcia obrazka.
W linku bardziej czytelna wersja: czerwonymi punktami oznaczyłem Hetmany, które zamieniają się miejscami z najbliższymi sąsiadami.
https://www.fotosik.pl/zdjecie/31f292cad92c92e4
Jetem pewien, że pięknie Pan to poukłada – za co dziękuję 🙂
Właściwie już jest przejrzyście i pięknie ułożone. Dzięki.
mp
Ogólnie (nie wnikając w nieistotne dla idei szczegóły):
Dla każdego rozmiaru planszy N:
W przypadku przesuwania nieparzystej liczby N Hetmanów minimum można obliczyć jako:
N-1+sqrt2
Dla parzystych jest to N
Czyli nieparzyste wymagają jednego kroku ukośnego.
Mnie się wydaje, że to trzeba by sprawdzić wszystkie przypadki wyboru trzech z dziewięciu, czyli to jest symbol Newtona 9 nad 3, 9*8*7/(1*2*3) = 3*4*7 = 84. Niby nie tak dużo… zapewne wiele odpadnie, ponieważ pozostała szóstka tworzy „sieć rażenia” i nie każda trójka może się dać poprzestawiać, nie ryzykując starcia z hetmanem z wrażej szóstki. No ale to się oczywiście średnio chce wszystko sprawdzać, należy podążyć za wskazówką, podaną w przykładzie, tym z 8,4. Można wziąć tę samą trójkę, ale przesunąć z f6 na g6, z d9 na d8, i trzecie zostaje z g8 na f9. Mamy 1+1+sqrt(2), no to mniej się chyba już nie da. Dałoby się ewentualnie 1+1+1, ale coś mi mówi, że przy dwóch jedynkach i takim przesuwaniu nie po skosie, trzecie przesunięcie musiałoby być o 2, na przykład c1-b1, b4-a4, a7-c7. Jedyne więc co jeszcze może się zdarzyć to 2+sqrt(2) dla jakiejś innej trójki, ale chyba nie zdążę już tego sprawdzić.
Odpowiadając na niezadane pytanie:
Czwarty układ w drugim wierszu (prawy dolny) obrócony o kąt 90 stopni przeciwnie do ruchu wskazówek zegara.
W linku wszystkie cztery możliwe rozwiązania zadania podstawowego:
(dowolny łączny dystans trzech przesunięć )
https://www.fotosik.pl/zdjecie/ff5168bc7f53a54f
Jedno z rozwiązań ma dystans minimalny czyli 2+sqr2
W poprzednim komentarzu link zawiera plik z błędem (powtórzenie).
Tu jest OK:
https://www.fotosik.pl/zdjecie/490d2b0846aaf282
Widzę teraz, że karanie ruchu ukośnego pierwiastkiem z 2, jakkolwiek jest pewną komplikacją, która nie wpływa na rozwiązanie, wskazuje liczbowo na obecność ruchu skośnego w rozwiązaniu minimalnym.
Fajne zadanie szachowe bo jest ono właściwie ogólne a tylko na bazie szachów. Dla wszystkich, nie tylko doświadczonych szachistów. Pewnie jest sporo ciekawych zadań w tym typie, np. z innymi figurami. Można by jeszcze czasem sięgnąć do tego arsenału…