Szum sum

21 sierpnia 2021
Marek Penszko

W zwykłym blokowisku każda skrajna liczba oznacza, ile bloków widać we wskazanym rzędzie, patrząc zgodnie ze wskazaniem strzałki. W blokowisku sumowym podana liczba jest sumą wysokości tychże widocznych bloków (pełny opis reguł – we wpisie sprzed 2 tygodni). Który rodzaj blokowiska jest zadaniem trudniejszym przy założeniu, że porównujemy dwa bliźniacze zadania, czyli w obu podanych jest przy brzegach tyle samo liczb i znajdują się one w tych samych miejscach – tylko ich wartości są oczywiście różne?
Uważam że blokowisko sumowe jest trudniejsze, ale nie jestem pewien, czy to stwierdzenie można uogólnić. Zwłaszcza że, co słusznie zauważył w komentarzu Michał, w przypadku sumy liczba możliwych rozmieszczeń bloków w danym rzędzie jest mniejsza, a więc tym samym droga do celu wydaje się jakby mniej wyboista. Z drugiej jednak strony istota zadania sprowadza się: po pierwsze – do zróżnicowania tych rozmieszczeń (gdy jest ich dużo, ale są do siebie bardziej podobne, to może być łatwiej o jednoznaczne wnioski) oraz po drugie – do ich „współdziałania” w wierszach i kolumnach. Wszystko to wydaje się nieco zawiłe, zatem w teorii trudno o pewne konkluzje.
Spróbowałem więc praktycznie sprawdzić jak to działa i przerobiłem sumowe blokowisko z poprzedniego wpisu na klasyczne. Inaczej mówiąc, sumy przy brzegach zastąpiłem liczbami widocznych bloków i w efekcie powstał poniższy diagram:

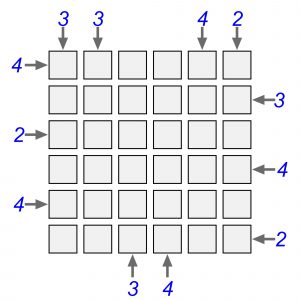
Zacząłem rozwiązywać to zadanie i po kilkunastu minutach… poddałem się. To znaczy dotarłem dość mozolną drogą do jednego rozwiązania – ale innego, niż to, które wynika z sumowego pierwowzoru. Być może jednak obrałem niewłaściwą drogę, więc nie będę zniechęcał do rozwiązywania. Odważnych i wytrwałych wędrowców logicznymi ścieżkami i błędnymi zaułkami prosiłbym tylko o informację, czy zadanie jest istotnie tak twardym orzechem, jak mi się wydaje oraz ile ma rozwiązań.

Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.