Blokersi sumują
Wprawdzie blokowisko już w Łamiblogu bywało, ale gwoli formalności przypomnę zasady zabawy.
Osiedle tworzy n2 prostopadłościennych bloków ustawionych w kwadrat n×n. Każdy blok składa się z 1≤s≤n jednakowych sześcianów – jakby kondygnacji, których liczba określa wysokość bloku. W każdym rzędzie i w każdej kolumnie stoi n bloków o różnych wysokościach – od 1 do n. Dla n=4 mamy praktycznie najmniejsze blokowisko, które może wyglądać jak na rysunku z lewej. Cyfry na dachach bloków oznaczają ich wysokości i tworzą kwadrat łaciński (rysunek po prawej).
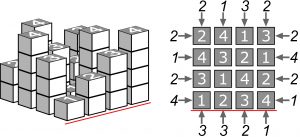
Liczby ze strzałkami wokół diagramu stanowią podstawę łamigłówki, która powstaje po usunięciu większości z nich oraz wszystkich wysokości bloków, jak np. na poniższym rysunku:
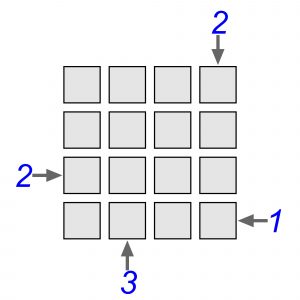
Każda liczba oznacza, ile bloków w danym rzędzie można zobaczyć z miejsca, w którym dana liczba się znajduje, patrząc zgodnie ze wskazaniem strzałki (wyższe bloki zasłaniają niższe). Na tej podstawie należy odtworzyć wygląd blokowiska, czyli wysokości wszystkich bloków.
Tę formalnie prostą, atrakcyjną i pomysłową łamigłówkę wymyślił przed 30 laty japoński nauczyciel matematyki w jednej ze szkół w Osace Masanori Natsuhara. Dekadę później holenderski łamigłówkarz Tim Peeters zaproponował równie atrakcyjny wariant blokowiska. Teoretycznie można weń przekształcić każde „klasyczne” zadanie, odpowiednio zmieniając liczby ze strzałkami. Odpowiednikiem powyższego rysunku byłby więc następujący:
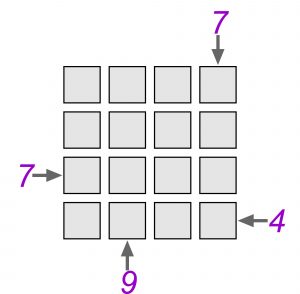
Każda liczba oznacza tym razem sumę wysokości widocznych bloków. Okazuje się jednak, że w tym przypadku wszystkie cztery liczby nie są konieczne. Którą z nich można usunąć bez utraty jednoznaczności rozwiązania?
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Rozwiązanie zadania:
2 4 1 3
4 3 2 1
3 1 4 2
1 2 3 4
Po usunięciu górnej siódemki nadal jest to jedyne rozwiązanie.
Po usunięciu dowolnej z pozostałych liczb pojawiają się dodatkowe rozwiązania.
Rozwiązanie
2413
4321
3142
1234
Można usunąć 7 u góry diagramu.
Można usunąć górną siódemkę.
Bez 7 u góry rozwiązanie też jest jedno.
Na pierwszy rzut oka wydaje się, że taka „zagmatwana” informacja jest mniej przydatna. Jest jednak inaczej. W przypadku klasycznym (ile bloków widać), mamy tylko cztery możliwe liczby 1, 2, 3 i 4. A przy sumowaniu jest więcej możliwości, bo sumami mogą być wszystkie liczby od 4 do 10. Na każdą przypada więc średnio mniej możliwych układów bloków, dzięki czemu łatwiej o jednoznaczność przy mniejszej liczbie informacji.
Górna 7 jest nadmiarowa.
Górnej siódemki może nie być.
górną 7.
Siódemka na górze jest zbędna.
2413
4321
3142
1234
Można usunąć siódemkę nad czwartą kolumną i nie wpłynie to na jednoznaczność odpowiedzi.
Gdybyśmy natomiast usunęli:
1) Siódemkę z lewej strony trzeciego wiersza, uzyskamy takie alternatywne rozwiązanie:
2) Dziewiątkę spod drugiej kolumny, uzyskamy takie alternatywne rozwiązanie:
3) Czwórkę z prawej strony czwartego wiersza, uzyskamy takie alternatywne rozwiązanie:
7-ka nad kolumną „d” niepotrzebna.
Małe blokowisko, jednak nie ściernisko.
Co będzie, gdy pojawi się San Francisco?