Światłocień
Wprawdzie xswedc na pewniaka podał poprawne rozwiązanie zadania z poprzedniego wpisu, ale pełnej instrukcji obsługi w komentarzach zabrakło, więc wypada, aby się pojawiła. Oto ona.
W niektórych białych polach należało umieścić żarówki (kółka). Każda oświetla ciąg białych pól w rzędzie i kolumnie, na przecięciu których się znajduje, ale zasięg światłości ograniczają czarne pola, które „wystają” z diagramu, więc za każdym oświetlonym po przeciwnej stronie pojawia się cień (szare pola), ciągnący się do następnego czarnego kwadratu lub do brzegu diagramu. Cień znika z pola oświetlonego przez inną żarówkę, a nieoświetlone pola też pozostają białe. Dwie żarówki nie mogą na siebie świecić.
Tyle w ramach uzupełnień. Bieżący temat jest podobny, bo na diagramie także pojawiają się światła (białe pola) i cienie (szare), ale w znaczeniu artystycznym – jako jasne i ciemne fragmenty „obrazu” – zatem żarówek brak. Łamigłówka także, jak poprzednio, jest indugadką, czyli poniższy przykład powinien wystarczyć do poradzenia sobie z zadaniem.
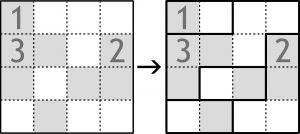
A zadanie wygląda tak:
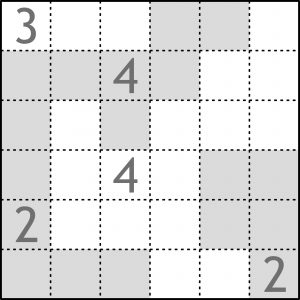
Z przykładu od razu widać, że chodzi o podzielenie diagramu na części (wielokąty). Przyglądając się nieco uważniej podziałowi, nietrudno wyindukować więcej, a nawet wszystko.
W rozwiązaniu wystarczy podać liczbę części, na które podzielony został diagram, łamaną przez liczbę boków największej części. Dla przykładu rozwiązaniem byłby więc ułamek 5/10 (wyjątkowo nieskracalny).
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
7/10
0.6
Podzieliłam ten diagram na 3 sposoby. Pewnie tylko raz dobrze (a może wcale). Co ciekawe, za każdym razem odpowiedź wyrażona ułamkiem brzmi tak samo.
Gdyby czwórka z pola c3 była jedynką, to moja odpowiedź brzmiałaby 6/8.
Czwórka z c3 istotnie mogłaby być jedynką, ale wtedy odpowiedzią nie byłoby 6/8.
mp
8/12
Diagram należy podzielić na obszary składające się z równych ilości białych i szarych kratek. Ilość kratek białych i szarych określa liczba zawarta w tym obszarze. Jeżeli powstanie obszar bez liczby to w nim jest jedna biała i jedna szara kratka. Białe i szare części w każdym obszarze są podobne (z dokładnością do obrotów).
Instrukcja PRAWIE dobra i odpowiedź też PRAWIE (zły „licznik”).
mp
9/12
8/10
Najpierw odniosę się do odmiany zaproponowanej przez apartado, bo jestem najbardziej pewien tego rozwiązania. Jeżeli dobrze zrozumiałem zasady, to gdyby w polu c3 była jedynka zamiast czwórki – jak postuluje apartado – rozwiązaniem byłoby 9/10, a podział wyglądałby tak:
http://ersonasolidna.pl/lamiblog/20210508_Swiatlocien/20210508_swiatlocien_apartado.png
OK!
mp
Jeśli chodzi o poprzednie zadanie z 1 maja i jego zasady, to dwie zasady były dość niełatwe do odgadnięcia:
– nieoświetlone pola też pozostają białe -> do tego można dojść analizując przykład
– dwie żarówki nie mogą na siebie świecić -> na to w ogóle nie wpadłem
Pozostałe zasady są dosyć klarowne, choć to, że żarówki oświetlają tylko pola w rzędzie i kolumnie, a nie na skos, nie jest do końca oczywiste, choć naturalnie wynikało z przykładu, a już wybitnie wynikało z samego zadania.
8/10
p.s. liczba oznacza spójny obszar biały lub szary, figura/cześć składa sie z dwóch róznokolorowych obszarów o tym samym kształcie. W zadaniu obie ‚4’ dotyczą tej samej figury/czesci.
Nie wypada się poddawać – tym bardziej, że dopiero środa – ale nie będę miał do soboty czasu już nad tym usiąść. Wychodzi mi albo 7/10 (co już wiemy, że jest błędną odpowiedzią po wpisie Oli GM) albo 8/10. Jednak 8/10 jest obarczone wadą – jeden z podziałów, z liczbą 4 w polu c3, zawiera figurę białą i figurę szarą, które się od siebie różnią kształtem. A wedle mojej inDuicji jedna z zasad gry mówi, że te kształty powinny być identyczne.
http://ersonasolidna.pl/lamiblog/20210508_Swiatlocien/20210512_swiatlocien_chybazle.png
Zakładam że objaśnienie zagadki brzmi:
„podziel obszar na fragmenty zawierające równą liczbę jasnych i ciemnych kratek – liczba w obszarze oznacza ile jest kratek jasnych/ciemnych, dodatkowo obszar z liczbą musi być spójny”
w takim przypadku rozwiązanie to 8/10
– nie wszystkie obszary mogą być spójne (nie ma rozwiązań głównego zadania)
– jeśli dopuścimy niespójność wszystkch obszarów – wtedy rozwiązań jest całkiem sporo.
obrazek (z kilkoma przypadkami): https://app.box.com/s/1fs49t4t3596zsvp81aiwj0rgfi85j2t
Spójność nie wystarcza, części powinny mieć taki sam kształt (z dokładnością do odbić i obrotów).
mp