Z łuskaniem
OlaGM rozwinęła skrzydła i nadesłała jeszcze jedno sumowo-iloczynowe zadanie, które określiła jako hardcorowe. Zasady zabawy pozostają niezmienione, czyli do dziesięciu pól należy wpisać dziesięć różnych liczb – od 1 do 10 – tak, aby w każdym wierszu i w każdej kolumnie znalazły się dwie liczby. Przed wierszem i nad kolumną podana jest suma lub iloczyn pary liczb, które powinny trafić do danego rzędu. Ekstremalność łamigłówki polega jednak na tym, że suma lub iloczyn nie jest konkretną liczbą – zamiast takowej wskazany jest zbiór liczb, w którym konkretny wynik się znajduje i trzeba go samodzielnie z tego mniejszego lub większego zbiorku wyłuskać.
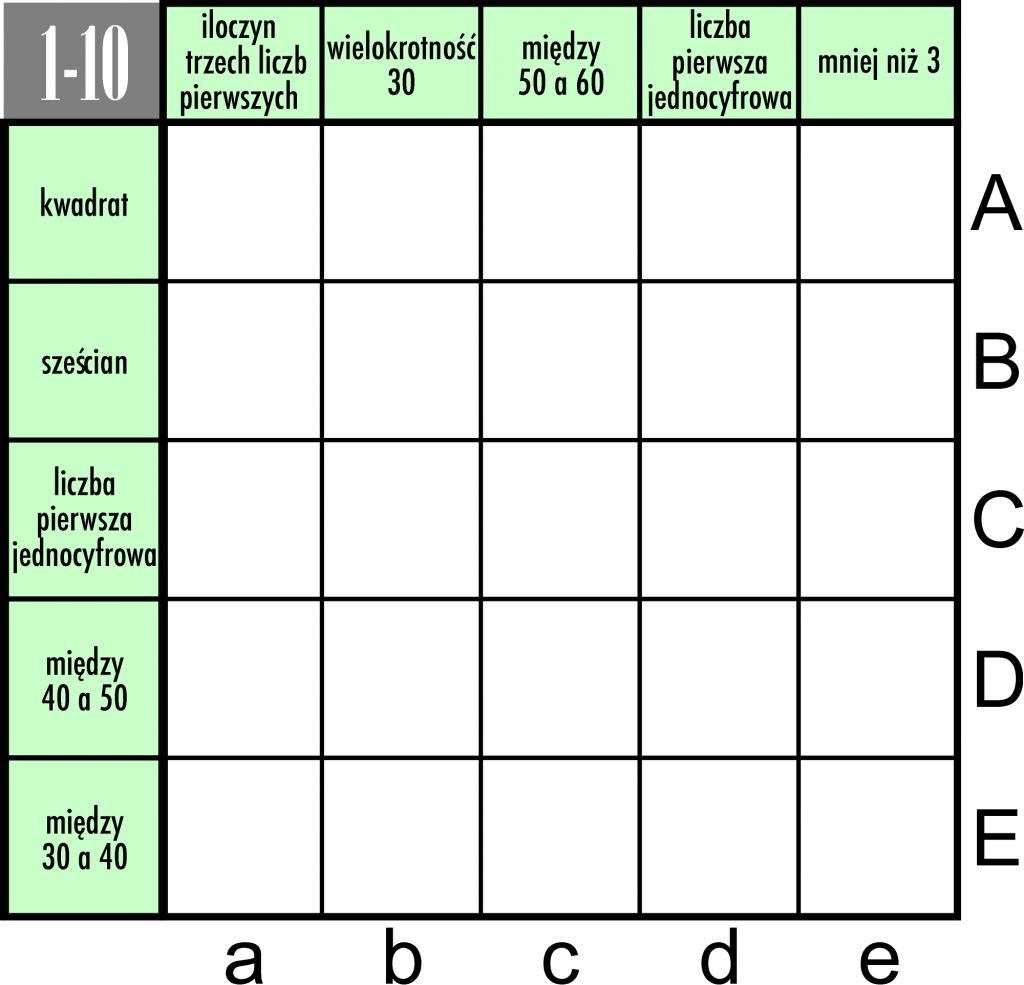
Łuskanie wymaga stosowania metody siłowej, czyli wypisywania prawie wszystkich możliwych par, ale – czego w poprzednim wpisie nie uwzględniłem – nie jest aż tak siłowe, czyli żmudne, jak w przypadku siłacza-komputera. Okazuje się bowiem, że rozwiązując zarówno poprzednie, jak i bieżące zadanie OliGM, można całkiem sprytnie, bo na logikę, eliminować niektóre uprzednio wypisane możliwe pary, dochodząc dość elegancko i „bezboleśnie” do jednoznaczności.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Hardcorowe raczej nie jest:
6 10 x x x
x x 7 x 1
x x x 3 2
5 9 x x x
x x 8 4 x
Dość szybko się wyjaśniają zwłaszcza kolumny, bo wiadomo, że w e tylko 1 i 2, a więc w d tylko 3 i 4 mogą być, 8 nie pasuje ani do a (samo w sobie jest iloczynem trzech liczb pierwszych), ani do b, więc w c 7 i 8, no i dopiero potem są dwie możliwości, czyli w b 6 i 10 a w a 5 i 9 (nie jest powiedziane, że mają być różne liczby pierwsze), lub w b 9 i 10, a w a 5 i 6. Czyli tu wchodzi metoda prób i błędów, ale do ogarnięcia, zwłaszcza gdy się uwzględni, że 10 i 6 ładnie pasuje jako kwadrat w pierwszym rzędzie.
x , x , 7 , x , 2 ,
x , 9 , x , 3 , x ,
5 , x , x , x , 1 ,
6 , x , 8 , x , x ,
x ,10, x , 4 , x ,
Jeśli przyjmiemy, że „między” oznacza słabą nierówność to jest OK. Tylko czy można tak przyjąć? Czy 1 i 2 są między 1 a 2? Albo czy usta i brzeg pucharu są między ustami a brzegiem pucharu?
mp
Ze słabą nierównością jest więcej rozwiązań. Z silną jeszcze nie wiem, ale jeśli powyższe jest jedynym, to troszkę boli kolumna ‚e’, gdyż jest tam i suma, i iloczyn. Tak, czy siak, Olga – masz talent.
6 ,10, x , x , x ,
x , x , 7 , x , 1 ,
x , x , x , 3 , 2 ,
5 , 9 , x , x , x ,
x , x , 8 , 4 , x ,
6,10,x,x,x
x,x,7,x,1
x,x,x,3,2
5,9,x,x,x
x,x,8,4,x
Przy uznaniu nierówności za słabe, mamy więcej rozwiązań, na przykład w rozwiązaniu @uch ty wystarczy zamienić miejscami 5 i 6. A dodatkowo, po zamianie 5 i 6, 8 można przesunąć w dół, a 10 odpowiednio w górę. Również w rozwiązaniu nazwijmy je niekontrowersyjnym, które w innym komentarzu, można dokonać podobnego przesunięcia.
6,10,X,X,X
X,X,7,X,1
X,X,X,3,2
5,9,X,X,X
X,X,8,4,X
@xswedc
Przyłączam się do pochwały pod adresem Autorki, ale w „e” nic chyba nie „boli”, bo ma być „mniej niż 3”, tu nierówność jest zdecydowanie ostra, i to daje tylko możliwość 1 i 2, przy czym 1*2 jest mniej niż 3, a 1+2 nie.
@aps1968
Fakt.
Poza tym pomyliłem OlaGM z Olga. Miałem gorszy dzień…