Qlisko bis

W każdym rzędzie (wierszu i kolumnie) kwadratu n×n leży n-1 kul różnej wielkości (o średnicach 1, 2, 3, …, n-1), a jedno pole jest puste (zerowe). Liczba obok danego wiersza lub nad (pod) kolumną oznacza, ile kul widzi obserwator stojący w tym rzędzie na polu zerowym plecami do liczby. Należy „uwidocznić” rozmieszczenie kul.
Poniższy przykład jest zadaniem z poprzedniego wpisu, a ściślej jego rozwiązaniem:

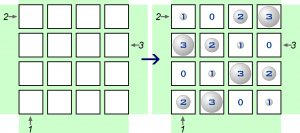
Bieżące zadanie jest tylko o jedno n większe:

I dodatkowe zadanie dla wytrwałych mistrzów: czy osiem liczb przy brzegach jest nadinformacją, tzn. czy po usunięciu którejś z nich (jeśli tak, to której?) zadanie nadal miałoby jedno rozwiązanie?

Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze

[xswedc]

  3  4  2  0  1 
  4  1  0  2  3 
  0  2  3  1  4 
  1  0  4  3  2 
  2  3  1  4  0 

Można pominąć dwójkę po prawej stronie.

[kerajs]

3 4 2 0 1
4 1 0 2 3
0 2 3 1 4
1 0 4 3 2
2 3 1 4 0

Skreślenie prawej dwójki lub dolnej jedynki nie wpływa na jednoznaczność rozwiązania. Skreślenie innej liczby lub kilku liczb daje więcej niż jedno rozwiązanie.
PS
W zadaniu sprzed tygodnia skreślenie jednej, dowolnej liczby dawało jedno rozwiązanie.

[Michał S]

34201
41023
02314
10432
23140

[logi]

34201
41023
02314
10432
23140
Bez 2 z prawej strony drugiego wiersza od góry

[mag]

3, 4, 2, 0, 1
4, 1, 0, 2, 3
0, 2, 3, 1, 4
1, 0, 4, 3, 2
2, 3, 1, 4, 0
zadanie bardzo przyjemne dla oka i myśli

[uch ty]

Nadmiarowy liczbowskaz: „2 – wiersz 4”.