Mnożenie z oczkami
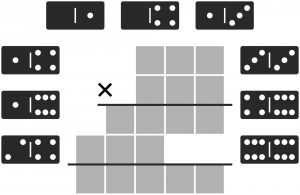
Jak już kiedyś wspomniałem, jestem „chory” na domino (między innymi), a ściślej – na zadania z dominem w roli głównej. Poniższa łamigłówka jest przejawem tej przypadłości. O co w niej chodzi – każdy widzi: z dziewięciu kamieni należy ułożyć słupkowy zapis mnożenia, którego sylweta majaczy między kamieniami, czyli parami cyfr. Uprzedzam, że zadanie jest dość żmudne, choć do ruszenia wyłącznie na logikę. Jego ewentualną zaletę stanowi połączenie kombinacji liczbowych z niewielkim udziałem geometrycznych.
![]()

Komentarze
341×106
341×106=36146
Ścieżka kombinacji geometrycznych okazała się, ku mojej radości, bardzo interesująca.
_ _341
x _106
———
_2046
341
———
36146
341*106
__abb
__acd
_efcd
gef__
ghhkk
Aby zadanie było rozwiązywalne kamienie można ułożyć tylko na 4 sposoby.
Ponadto od razu widać gdzie jest jedno z zer. Później tylko z górki.
341
106
2046
341
36146
341 * 106
a dokładniej jest tutaj
https://pokazywarka.pl/6xhup2/
Lubię zakończyć wątek jakąś refleksją.
Rozwiązanie to jest jedyne.
Jednym z podejść do tego zadania jest rozdzielenie go na dwa: a) numeryczne i b) geometryczne.
a) Z dostępnego zestawu cyfr na kamieniach domina można złożyć tylko jedno działanie spełniające warunki, właśnie 341 * 106.
Stwierdzenie tego jest nieco żmudne, ale pracę ułatwiają warunki zadania:
(jeśli mnożone liczby to A oraz B, to przez Ai i Bi oznaczam cyfry na pozycji 10^i)
– znamy multizbiór (element; krotność) dopuszczalnych cyfr
Z={(0;2);(1;,4);(2;1);(3;3);(4;4);(6;4)}
– wiemy że B1=0
– iloczyny B2*A0 oraz B0*A0 muszą dawać ostatnią cyfrę dopuszczalną, dodatnią.
b) Jeśli już znamy wszystkie liczby działania, część geometryczna -dopasowanie kamieni – jest czystą formalnością. Najłatwiej wyróżnić i zbadać 4 warianty w zależności od położenia kamienia zawierającego B1=0.