Efemeryda
Anatomia dzisiejszej łamigłówki sprzyja temu, aby przedstawić ją w formie indugadki, czyli zagadki indukcyjnej typu „dwa w jednym”. Zatem najpierw przykład z rozwiązaniem:
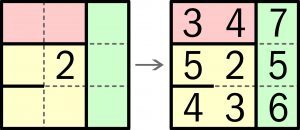
Z przykładu – to po pierwsze – należy odgadnąć (wywnioskować), jakie są zasady zabawy, a następnie – to po drugie – spróbować zastosować owe zasady w celu rozwiązania poniższej łamigłówki.
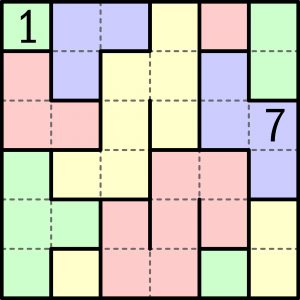
Podstawowe zasady są dwie – jedna łatwa do zauważenia, druga dość oryginalna, więc trudniej ją wykryć. W rozwiązaniu wystarczy podać sumę liczb na przekątnych. Nie zaszkodzi też pochwalić się rozszyfrowaną instrukcją obsługi.
Łamigłówka jest japońską efemerydą, która pojawiła się przed dekadą i żywot miała krótki, choć sporadycznie powraca.

Komentarze
Czy kreska między 4 a 5 w rozwiązanym przykładzie jest potrzebna?
Tak.
mp
Czy kolory mają pozaestetyczne znaczenie ?
Nie
mp
@mp
„Czy kolory mają pozaestetyczne znaczenie ?
Nie”
Jeśli nie, to na planszy są trzy niebieskie obszary?
Tak
mp
54
1. W każdym obszarze występują kolejne liczby.
2. Różnica pomiędzy sąsiednimi liczbami jest równa całkowitej długości kreski pomiędzy nimi.
Dodałbym jeszcze zasadę 0: Jeśli każda mapa może być prawidłowo pokolorowana czterema barwami, to mapa efemerydy również powinna.
Bingo! Kolory poprawiłem.
mp
135479
246368
435257
217474
435863
542352
Na przykładzie: bok zielonego prostokąta styczny do dwóch pozostałych ma długość 3, wiec różnica między sąsiednimi liczbami w różnych figurach jest 3. (7-4=3,5-4=3,6-3=3). Różowy prostokąt sąsiaduje z żółtym bokiem o dł. 2, wiec różnica między sąsiednimi liczbami =2. (5-3=2 i 4-2=2). Kreska w żółtym jest potrzebna,bo bez niej zamiast 5 mogłoby być 1
54
Trwało to długo, bo sądziłem, że liczby w kolumnach nie mogą się powtarzać (w przykładzie są one nawet kolejne !).
Definiowanie reguł pozostawiam fachowcom od definiowania reguł.
@mp
„Czy kolory mają pozaestetyczne znaczenie ?
Nie”
„Jeśli nie, to na planszy są trzy niebieskie obszary?
Tak”
Jestem trochę zły na siebie, gdyż po dłuższym (niestety) namyśle zauważyłem, że odpowiedź na moje pytanie jest do wydedukowania po poprzedniej odpowiedzi na pytanie @apartado, a wynika z tego, że plansza jest… obramowana. Przepraszam za wymuszenie niepotrzebnej zmiany barw obszarów. Ot, stupor…
Zauważam jednak, że gdyby powstrzymał się Pan od odpowiedzi zarówno na pytanie @apartado, jak i moje, to zadanie byłoby ciekawsze. Zadania z niejednoznacznościami, błędami, niedomówieniami są dla mnie bardziej interesujące, gdyż wtedy należy po pierwsze stwierdzić „babola”, a po drugie znaleźć, mimo to, prawidłowe rozwiązanie. W przypadku japońskiej efemerydy, przy dwóch obszarach niebieskich, prawidłowego rozwiązania nie ma. Jedna z liczb (nie cyfr!) powtarza się dwukrotnie w tym większym niebieskim (według pierwotnej kolorystyki) obszarze.
Zadanie dla pasjonatów: jaka liczba i w których polach (notacja jak na szachownicy) się wtedy powtarza?
Kolory zmieniłem z przyjemnością – wyłącznie ze względów estetycznych.
Nie rozumiem wpływu kolorów na rozwiązanie.
mp
@mp
„Nie rozumiem wpływu kolorów na rozwiązanie”.
Przy założeniu, jak już wiadomo – błędnym, że to barwy określają obszary, to w pierwotnej wersji kolorystycznej niebieskie obszary były dwa, przy czym ten większy miał 11 pól. I z tym się zmagałem. Szkoda, że nie było rozwiązania…
W części pierwszej spróbuję rozwikłać regułę: po pierwsze, w każdym kolorowym fragmencie o polu n kratek ma być n kolejnych liczb naturalnych. Po drugie, na polach oddzielonych grubą kreską o całkowitym boku k, występują liczby różniące się o k. W przykładzie, jak i w zadaniu, k jest równe 1, 2 lub 3.
Sumy na diagonalach to 22 i 32
czyli coś takiego?
https://pokazywarka.pl/u9ske7/
WSKAZÓWKA: Kilka odcinków temu na tym blogu gościła inna japońska łamigłówka, która też nie przyjęła się, a podobieństwa między nimi sięgają głębiej.
I wielka szkoda, że się nie przyjęły, bo to b. interesująca alternatywa dla Sudoku i innych krzyżówek numerycznych.
W części drugiej, rozwiązanie na podstawie reguły przedstawionej w części pierwszej:
1 3 5 4 7 9
2 4 6 3 6 8
4 3 5 2 5 7
2 1 7 4 7 4
4 3 5 8 6 3
5 4 2 3 5 2
Wygląda na to, że jest jedno rozwiązanie, w dodatku rozwiązywanie nie było wcale takie proste, co mnie przekonuje, że zarówno reguła, jak i rozwiązanie, są w porządku. Suma na przekątnych wychodzi 54.