Koko

8 listopada 2018
Marek Penszko

Łamigłówki przesuwanki często są odwracalne. Gdyby tę sprzed dwóch tygodni „puścić od tyłu”, wyglądałaby tak:

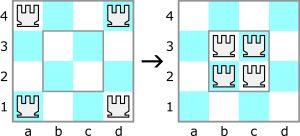
Zadanie polega na wykonaniu serii ośmiu ruchów, po których wszystkie cztery figury znajdą się na czterech centralnych polach. Każdy ruch powinien być przesunięciem którejś figury w rzędzie lub kolumnie, ale zawsze na pole sąsiadujące w rzędzie lub kolumnie z polem zajętym przez jakąś inną figurę. Dwa lub więcej kolejnych przesunięć tej samej figury stanowi jeden ruch.
Ze względu na symetrię zacząć można od jednego z ośmiu „bliźniaczych” przesunięć. Jeśli wybierzemy 1. a1-c1-c4, to bliźniacze będzie – w stosunku do zadania sprzed dwóch tygodni – całe rozwiązanie, ale zapisane wspak: 2. a4-b4  3. c4-c1  4. d1-d3-b3  5. d4-c4-c3  6. c1-c2  7. b3-b2  8. b4-b3.
Zadanie z dośrodkowym ruchem figur wydaje się trudniejsze niż poprzednie z ruchem do rogów, mimo że różnica jest czysto formalna. Figury są wieżami szachowymi nie tylko dlatego, że wykonują wieżowe ruchy, ale także ze względu na bliższe koligacje szachowe.
Przed 30 laty niemiecki problemista Heinz Zander wymyślił wariację szachową zwaną koko (skrót od „kolońskie kontaktowe szachy”), która szybko zyskała sporą popularność w nieortodoksyjnej, czyli tzw. bajkowej kompozycji szachowej. Jej podstawę stanowiła niemal dokładnie taka sama zasada, jak w powyższej przesuwance: ruch można wykonać tylko na takie pole, które sąsiaduje (w tym wypadku bokiem lub rogiem) z polem zajętym przez inną bierkę dowolnego koloru. Ta reguła skutkuje kilkoma osobliwymi odstępstwami od klasycznej gry. Na przykład, nie można zbić bierki, koło której nie stoi żadna inna bierka. Dotyczy to także króla, który nie jest szachowany, jeśli nie ma obok siebie towarzystwa. Z drugiej strony jeśli król zostanie zaszachowany, a on sam albo towarzysząca mu bierka ma możliwość odejścia tylko na odosobnione pole, czyli praktycznie brak jest ruchu (i innych możliwości obrony też) – to taka pozycja stanowi mat. Ponadto dwa króle mogą stać obok siebie, jeśli obok żadnego z nich nie ma innej figury albo jeśli figura stoi tylko obok jednego z nich – wówczas jest szach królem (szachowany jest ten z sąsiednią figurą). Natomiast niedopuszczalna jest pozycja równorzędna, czyli aby oba sąsiadujące króle miały sąsiada. Takie zawiłości umożliwiają układanie ciekawych zadań.

Oto przykład koko dwuchodówki, czyli po ruchu białych i odpowiedzi czarnych białe powinny zamatować czarnego króla.

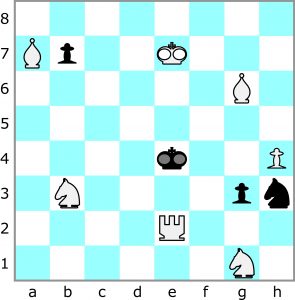
W zwykłych szachach sytuacja przed ruchem białych taka, jak na diagramie – szachowanie czarnego króla (zwłaszcza równocześnie przez dwie figury, wieżę i gońca) – byłaby niemożliwa. W koko król nie jest szachowany, bo nie ma obok siebie żadnej bierki.
Rozwiązanie zadania rozpoczyna ruch gońca: 1. Ga7-b8, po którym czarne muszą wykonać jedno z pięciu możliwych posunięć: g3-g2, Sh3-f2 lub g5, Ke4-e3 lub f5; ruch pionem b7 jest teraz niewykonalny, bo pion traciłby kontakt z inną bierką, zaś skok Sh3-f4 to „samobój” (król wpada w szach). Na każdą z podanych wyżej możliwości czarne odpowiadają matem gońcem lub wieżą. Po g3-g2 następuje 2. Gb8-f4X; po Sh3-f2 – 2. Gg6-f5X; po Sh3-g5 – 2. We2-e3X; po Ke4-e3 – 2. Gg6-e4X; po Ke4-f5 – 2. We2-e4X.
Poniższe zadanie jest trzychodówką, czyli białe matują w swoim trzecim posunięciu.

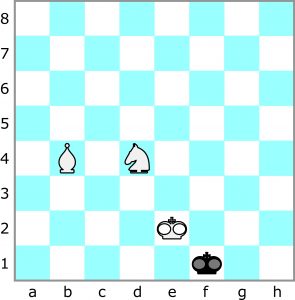
Mimo większej liczby ruchów zadanie jest prostsze, bo jednowariantowe, a ruchy czarnego króla są wymuszone. Białe także mają niewiele możliwych pierwszych ruchów – dokładnie osiem. Który pierwszy ruch jest właściwy? Całe rozwiązanie także będzie mile widziane.