Wskazówki
Pisałem kiedyś o zadaniach, zawierających liczby i strzałki sprzężone, czyli stanowiące razem jeden element, który nazwałem „listem” (od początkowych par liter słów „liczba” i „strzałka”), choć chyba zamiast „listów” lepsze byłyby „cysty” (gdyby się źle nie kojarzyły), bo liczby w tych zadaniach zawsze są cyframi. Jest też sporo rodzajów łamigłówek, w których cyfry i strzałki są ze sobą luźniej powiązane. Oto przykład jednego z nich, mało znanego, bo uchodzącego za bardzo trudny.
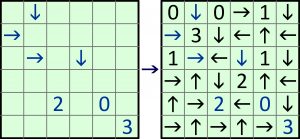
W każdej kratce powinna pojawić się cyfra lub odpowiednio skierowana (N, W, S lub E) strzałka. W niektórych znaki już są. Pozostałe kratki należy wypełnić tak, aby spełnione były następujące warunki:
– w polach sąsiadujących w rzędzie lub kolumnie nie mogą znaleźć się dwie cyfry albo dwie strzałki wskazujące w tym samym kierunku;
– każda cyfra (liczba) powinna być równa liczbie wskazujących na nią strzałek w wierszu, a także liczbie wskazujących na nią strzałek w kolumnie;
– każda strzałka musi wskazywać na jakąś cyfrę.
Jeśli w kierunku, w którym wskazuje strzałka, jest więcej niż jedna cyfra, to za wskazaną uznaje się tylko tę najbliższą.
Przykład
Zadanie
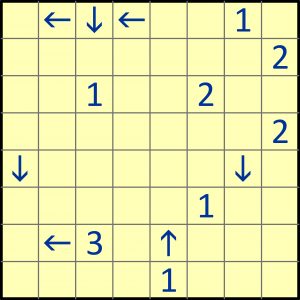
Zmagania z tym zadaniem łatwo zacząć, ale niebawem pojawiają się strome schody, więc trzeba sporo wytrwałości, aby dotrzeć do ostatniego stopnia. W rozwiązaniu wystarczy podać sumę wszystkich cyfr (liczb) oraz liczbę strzałek wskazujących na wschód :).
![]()

Komentarze
W temacie cyfra vs. liczba jestem bardzo wyczulony.
Dziękuję za to, że w tym wpisie zostało to wyróżnione.
Miodziu lubi to!
Liczba, nawet jednocyfrowa, nie przestaje być liczbą.
Użyte tu obiekty to liczby (zapisane przy pomocy cyfr).
Suma: 21
Strzałki wschodnie: 13
Wschód OK, suma nie taka.
mp
Jest taki moment właściwie tuż przed metą, że niemal traci się już wiarę w sens całej tej logiki (zapachniało porażką), ale po chwili wszystko się wyjaśnia – w ostatniej chwili nadchodzi pomoc – dla tego momentu warto przez to przejść.
https://prnt.sc/jophuc
Taki suchar mi się przypomniał:
Idzie student fizyki ulicą, zaczepia go babka:
– Do kościoła to dobry kierunek?
– Dobry – odpowiada student.
Babka odchodzi, a student do siebie:
– Kierunek dobry, ale zwrot przeciwny.
Kwestia sum: przeoczona trójka zwiększa sumę do 24.
Ponieważ „student fizyki” podniósłby krzyk patrząc na przykład, ja tylko się upewnię co do znaczenia poniższego cytatu:
„w polach sąsiadujących w rzędzie lub kolumnie nie mogą znaleźć się dwie cyfry albo dwie strzałki wskazujące w tym samym kierunku”
a więc w wierszu nie może być obok siebie dwóch strzałek na wschód ale również nie może być obok siebie 2 strzałek np. na północ.
Mówiąc inaczej, „kierunek” (a raczej zwrot 😉 ) jest wyznaczany przez strzałki a nie wiersz bądź kolumnę w której te strzałki się znajdują.
Oczywiście, wykluczamy zgodność kierunku (raczej nie zwrotu – to nie są wektory tylko kierunkowskazy) wskazywanego przez sąsiednie strzałki – bez względu na ich umiejscowienie.
mp
Wyskoczył nam zabawny problem używania ugruntowanych symboli ścisłych pojęć do oznaczania pojęć z języka potocznego.
Powstaje pytanie filozoficzne: jeśli kierunkowskaz wygląda jak wektor swobodny to czy w pewnym sensie nim się nie staje ?
Ale niech to pozostanie wątkiem drugorzędnym tego trudnego zadania 🙂
Podobieństwo każdego A do jakiegoś B „w pewnym sensie” utożsamia A z B.
mp
Przepraszam, ale wyjaśnienie p. Marka pod postem Spytka jest „zaciemnieniem”. Wykluczamy tylko identyczność strzałek w sąsiadujących polach czyli w języku studenta fizyki – zgodność kierunku i zwrotu. Strzałki o zgodnym kierunku mogą sąsiadować jeśli tylko mają przeciwne zwroty (por. przykład).
Spytku, czy istotnie „zaciemniłem”? Chciałem dobrze 🙁
mp
Jeśli się nie grzmotnąłem to
∑ 24
#► 13
albo skorzystam z tożsamości: 1 obraz = 1000 słów
http://pokazywarka.pl/yz129n/
Wygląda na to że, mamy w tej chwili dwa dobre rozwiązania, czyli na podium rozdano już złoto i srebro.
Przez chwilę zastanowiłem się, kto będzie tą trzecią osobą i pomyślałem: „dziewczyny lubią brąz” i już wszystko jasne 😉
Przynajmniej dwa.
mp
2×3+4×2+10×1=24
Na wschód 13 strzałek, na zachód 11, na północ 11 i na południe 13 strzałek.
Spróbuję to ująć najkrócej jak się da:
W wierszu (ani w kolumnie) nie może być następujących sąsiadów: NN,WW,SS,EE.
@Spytko
W matematyce „najkrocej” najczęściej oznacza „najlepiej”.
Powyższe popieram artykułem: http://www.deltami.edu.pl/temat/matematyka/logika/2012/07/30/Niemozliwy_skrot/
Suma liczb: 24. Przy zadaniu nie ma informacji o położeniu stron świata, ale podejrzewam, że na wschód oznacza w prawo, więc 13.
Panie Marku, czy mogę zadać pytanie z innej beczki?
Chciałabym nawiązać do wpisu sprzed… 10 lat. Pisał Pan wtedy o Ryucie Kawashimie, który opracował książeczkę z ćwiczeniami usprawniającymi i odmładzającymi umysł.
Czy ma Pan może jakiś zestaw ćwiczeń Kawashimy? A może ktoś z uczestników Łamibloga ma i się ze mną podzieli?
Mam taki plan, że poćwiczę i poprawię sobie pamięć 🙂
Pani Olu, nie dysponuję ćwiczeniami Kawashimy w formie elektronicznej. Mam jego dwie książki „Train your brain…”, które są dostępne np. na Amazonie. Jest także seria jego ćwiczeń „Brain Age” w postaci gier wideo https://en.wikipedia.org/wiki/Brain_Age
mp