Nie tylko CBA
Literama (zadanie plus rozwiązanie) wygląda na przykład tak:
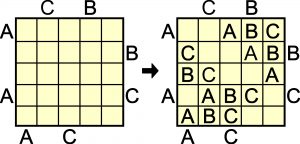
Przypomnę o co chodzi w tym przypadku.
W kratkach należy rozmieścić litery ABC tak, aby w każdym rzędzie (wierszu i kolumnie) znalazły się trzy różne. Liter jest mniej niż kratek, więc dwa pola w każdym rzędzie zostają puste. Kluczem do rozwiązania są literowe podpowiedzi przy brzegach – każda jest taka, jak najbliższa litera w rzędzie, przy końcu którego podpowiedź się znajduje.
A teraz niby to samo, ale trochę inaczej.
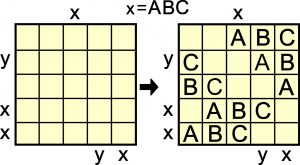
Tym razem przy brzegach są niewiadome. Każda z nich określa konkretny ciąg trzech liter w danym rzędzie, czyli ich kolejność – patrząc od niewiadomej wzdłuż rzędu lub kolumny (teoretycznie niewiadomych może być sześć). Ponadto x zawsze oznacza ciąg ABC. Jakie ciągi oznaczają pozostałe niewiadome – nie wiadomo. W przykładzie y=CAB.
W zadaniu niewiadome jako symbole są trzy, a w rzeczywistości dwie, bo – przypominam – x jest znane, równe ABC.
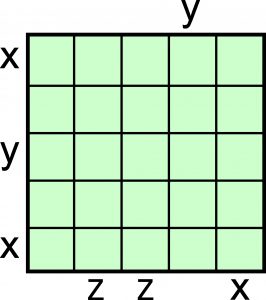
Jako rozwiązanie wystarczy podać ciągi-niewiadome y i z.

Komentarze
x=ABC
y=BAC
z=BCA
Rozwiązanie (X puste)
XXABC
CXXAB
BACXX
XCBXA
ABXCX
Zadanie troszkę trudniejsze od zwykłej literamy.
Y = BAC
Z = BCA
y = BAC
z = BCA
– – A B C
C – – A B
B A C – –
– C B – A
A B – C –
Y=BAC, Z=BCA
XXABC
CXXAB
BACXX
XCBXA
ABXCX
W ramach ciekawostki… no właśnie, nabyłem sobie „Ciekawostki matematyczne” I. Lehmanna i A. Posamentiera, pośrednio zachęcony przez rubrykę „Umysł giętki”.
Obietnica autorów to proste zagadki o zaskakujących rozwiązaniach. Czy została spełniona? Za wcześnie na ocenę bo ledwo ją kupiłem, ale obawiam się iż miłośnicy Łamibloga mogą uznać niektóre zadania za nieco trywialne. Nadal jednak jest to skarbnica fascynujących problemów, czasami z efektem „zonk!”. Oto przykład (po mojej lekkiej modyfikacji):
Do suszarni owoców trafiła tona winogron o zawartości wody 99%. Ile ważą owoce po osuszeniu, jeśli w wyniku tego procesu zawartość wody spadła do 98%?
Spróbuj udzielić szacunkowej odpowiedzi „w rozumie” zanim sięgniesz po kartkę czy kalkulator.
Jest tu efekt zonk!… chyba że ktoś pracował przy produkcji rodzynek. Ten efekt nazwałbym „ruchomą bazą”. Umysł idzie na łatwiznę i trzyma się stałej bazy (sto części). Nawet jeśli ma świadomość jej zmienności, to nie mogąc w pamięci oszacować ułamka typu 98/99 stosuje kiepskie zaokrąglenie (98/100) zamiast dobrego (99/100). Odparowanie 1/100 części wody praktycznie nie zmieni jej udziału (98/99 ≈ 98,99%), nawet odparowanie 1/10 (89/90 ≈ 98,89%).
Od kilkunastu lat, czyli od czasu publikacji w książce Davida Darlinga „Universal Book of Mathematics…” (2004), zadanie to jest określane jako „kartoflany paradoks” https://en.wikipedia.org/wiki/Potato_paradox. Znane jest jednak znacznie dłużej w różnych wersjach owocowych, warzywnych lub grzybowych – ja znam je od lat 70. z truskawkami, ale nie pamiętam skąd. Próbowałem ustalić, kto i kiedy je wymyślił. Bezskutecznie. Gdyby ktoś z Państwa trafił na jakieś chociaż półwiekowe źródło tej łamigłówki, wdzięczny będę za informację.
mp
Y=BAC
Z=BCA
Ciągi znalazłem nadspodziewanie szybko, po nieskomplikowanym wnioskowaniu – pomogło „domniemanie”, że ciągi się nie powtarzają.
Dopiero później zbadałem, czy ten zestaw jest prawidłowy (czy pasuje do diagramu).
PS. Jeśli ktoś pracował przy produkcji rodzynek to wie, że trzeba się skupić na suszu, nie na wodzie 🙂
XXABC
CXXAB
BACXX
XCBXA
ABXCX
y=BAC
z=BCA
przed:
990 kg – woda (99%)
10 kg – susz (1%)
po:
490 kg – woda (98%)
10 kg – susz (2%)
Fantastyczne zadanie! Faktycznie, trzeba było skupić się na suszu.
Tylko nie CBA! Już lepiej Y = BAC oraz Z = BCA.
PS. Dość złożona strategia a można rozwiązać w kilku logicznych krokach. No ale w końcu to są łamigłówki logiczne 😉
y=BAC, z=BCA
Jestem prawie pewny, że to zadanie w wersji truskawkowej było opublikowane
w Rewii Rozrywki w roku 1977 albo 1978. Ponieważ Rewia była wtedy kwartalnikiem to należy przejrzeć w najgorszym przypadku 8 numerów. Ja tego nie mogę sprawdzić, ponieważ w wyniku przeprowadzek stare roczniki Rewii gdzieś mi się zawieruszyły. Zadanie to zapamiętałem, bo próbowałem je wówczas na moich kolegach z I (II) roku studiów na Politechnice Wrocławskiej (efekt zonk! był).
Dziękuję za info, choć to niewiele wyjaśnia, bo zadanie w Rewii sam zamieściłem (pracowałem wówczas w redakcji „Rozrywki”), ale oczywiście nie wymyśliłem. Skąd zaczerpnąłem pomysł – nie pamiętam, ale podejrzewam jakieś rosyjskie źródło (Perelman, Kordiemski), bo u anglosaskich klasyków (Loyd, Dudeney) go nie uświadczyłem.
mp
Kordiemski chyba nie wymienia takiego zadania. Głowy nie dam ale przekartkowałem i nie znalazłem.
Podlinkowany przez Pana Marka artykuł z Wikipedii zwraca uwagę na to, że gdyby woda stanowiła najpierw 99,999% zawartości, a po wysuszeniu 99,998% zawartości, liczba kilogramów również zredukowałaby się o połowę. Matematyka bezwzględnie wygrywa z intuicją.
Jeśli stały składnik zwiększył udział dwukrotnie, to całość musiała schudnąć o połowę. „Bezwzględność” to właściwe słowo oraz cecha matematyki.
Mam wrażenie, że dawno temu, chyba w latach 80-tych, spotkałem się z tą zagadką w wersji grzybowej. Ciekawe czy uda się wyśledzić jej źródła…
Chyba jedno z łatwiejszych zadań w Łamiblogu ever 🙂 od góry rzędami: ooACB, CooAB, BACoo, oCBoA, ABoCo, czyli y jest BAC, a z BCA.
Co do zadania Markoniusza, to przyznam, że nie miałem żadnych wstępnych intuicji, wyszedłem „od suszu” jak należało, i wynikiem nie byłem specjalnie zaskoczony. No, może trochę.