Trzy po trzy Fareya
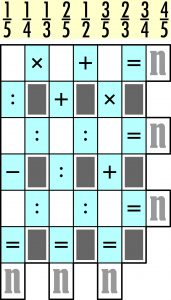
Do białych pól diagramu należy wpisać dziewięć umieszczonych nad nim ułamków – tworzą one tzw. ciąg Fareya F5. Ich rozmieszczenie powinno być takie, aby w wierszach i kolumnach powstały poprawne działania, a wynikiem każdego powinna być liczba naturalna n. Działania w rzędach należy wykonywać po kolei, czyli bez uwzględniania pierwszeństwa mnożenia i dzielenia (uwaga ta dotyczy praktycznie tylko środkowej kolumny).
Jeszcze dodatkowa uwaga (po uwadze Czytelnika): w zadaniu nie jest powiedziane, że wynik każdego działania powinien być taki sam. Powinien być tylko zawsze liczbą naturalną n (litera n oznacza każdą liczbę naturalną).

Komentarze
Ojoj… To zadanie ze Świata Nauki. Przez 3 tygodnie probowalem je rozwiązać i doszedłem do wniosku, że treść jest nieco myląca…
Ostatecznie znalazłem tylko jeden układ ulamkow, w którym wynikiem każdego z 6 działań jest liczba całkowita. Jednak nie jest to jedna liczba, lecz kilka różnych liczb.
A diagram sugeruje, że jest jedna liczba całkowita n, która jest wynikiem każdego z działań.
„…uwaga ta dotyczy praktycznie tylko środkowej kolumny…” ale również 2 i 3 wiersza gdyż (8:4):2=1 ale 8:(4:2)=4 🙂
🙂
mp
@Gospodarz
Nie moge sie zgodzic ze stwierdzeniem:
„w zadaniu nie jest powiedziane, że wynik każdego działania powinien być taki sam.”
To jest powiedziane:
„a wynikiem każdego (dzialania) powinna być liczba naturalna n.”
Gdyby w powyzszym cytacie usunac ostatnia litere „n”, to wtedy byloby ok. Ale ta litera sugeruje, ze jest jedna liczba naturalna (nazwana przez autora zadania jako „n”), ktora jest wynikiem kazdego z dzialan.
A co o tym sadza inni czytelnicy?
@Spytko z Melsztyna
Z Toba rowniez nie moge sie zgodzic. Piszesz:
„…ale również 2 i 3 wiersza gdyż (8:4):2=1 ale 8:(4:2)=4”
Masz racje, gdyz druga czesc Twojej wypowiedzi jest prawdziwa.
Ale Gospodarz swiadomie zaznaczyl, ze uwaga dotyczy tylko srodkowej kolumny, bowiem tylko w tej kolumnie standardowa kolejnosc wykonywania dzialan jest inna niz zamierzona przez autora zadania.
W wierszu 2 i 3 mamy dzialania postaci x:y:z, ktore standardowo interpretuje sie jako (x:y):z – bo tak wynika z pierwszenstwa wykonywania dzialan i tak tez jest zalozone w tej lamiglowce – dlatego w tych wierszach nie trzeba dodawac wyjatku, ktory autor musial dodac dla srodkowej kolumny.
Idac dalej tym tropem powinnismy sie czepic rowniez pierwszego wiersza: przeciez (3*2)+1 = 7, ale 3*(2+1)=9.
I dalej pierwszej kolumny: (8:4)-2=2, ale 8:(4-2)=4.
I jeszcze dalej w trzeciej kolumny analogicznie jak w pierwszym wierszu: (3*2)+1 = 7, ale 3*(2+1)=9.
Rozwiazanie:
3/5 1/3 4/5
1/2 2/3 3/4
1/5 1/4 2/5
Wyniki dzialan w wierszach to (1, 1, 2), natomiast w kolumnach to (1, 4, 1).
Jest tylko jedno rozwiązanie:
http://pokazywarka.pl/oh22nk/
@miodziu
Moja uwaga (dot. wierszy 2 i 3) była skierowana do tych, którzy nie uważają za oczywiste, że dla działań o tym samym priorytecie stosujemy porządek od lewej do prawej.
Że tacy osobnicy istnieją możemy się dowiedzieć np. stąd:
https://pl.wikipedia.org/wiki/Kolejno%C5%9B%C4%87_wykonywania_dzia%C5%82a%C5%84
Autorzy odnotowują tam fakt, że jedne kalkulatory traktują zapis a^b^c jak (a^b)^c a inne jak a^(b^c).
Do komentarza @miodzia dotyczącego uwagi @Gospodarza odnośnie liczby naturalnej n.
Zgadzam się z miodziem.
Liczba naturalna n
oraz
liczba naturalna,
to jednak, w kontekście tego zadania, nie jest to samo.
W powyższym zadaniu nigdzie nie jest powiedziane jak powinniśmy, wg @Gospodarza, rozumieć określenie „liczba naturalna n”, więc nie pozostaje mi nic innego jak przyjąć wyjaśnienie @miodzia.
Zajrzałem do „Umysłu giętkiego” 02/2018, skąd pochodzi to zadanie, a tam, w treści zadania, nie ma określenia „liczba naturalna n”, a zamiast tego jest „liczba naturalna”.
Więc nie powinno być problemu ze zrozumieniem zadania.
Pewne wątpliwości może budzić litera „n” występująca na rysunku, jako, no właśnie, jako co?
Czy „n” z diagramu oznacza, dowolną liczbę naturalną, jedną (taką samą) liczbę naturalną, a może jest to tylko ozdoba, żeby rysunek ładniej wyglądał?
I czasami z takich wątpliwości, co jest urokiem łamigłówek, biorą się różne odpowiedzi.
Wysoki Sądzie, czy określenie „liczba naturalna n” w tym zadaniu można uznać za równoznaczne z określeniem „taka sama liczba naturalna n” w takim stopniu, że odpowiedź „zadanie nie ma rozwiązania” należałoby uznać za poprawną.
mp
Pragnę zwrócić uwagę na fakt, że litera N napisana jest stylizowaną czcionką i w dodatku jest szaro-burego nieokreślonego koloru co jednoznacznie ma wskazywać na dowolność jej wartości 😉
Jeżeli Czytelnik, będąc oczarowanym urodą diagramu, stwierdził, że zadanie nie ma rozwiązania, bo nie udało mu się znaleźć takiej samej liczby naturalnej n dla sześciu równań, to co należałoby zrobić?
Nie mnie to oceniać.