Jeszcze słupek
W piątym zimowym, a ogólnie trzynastym „Omnibusie”, który pojawił się przed świętami, jest następujące słupkowe zadanie.
Cyfry w zapisie poniższego mnożenia zastąpiono kratkami.
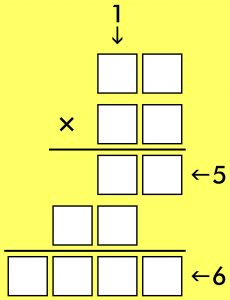
Należy rozszyfrować działanie, korzystając z podpowiedzi podanych przy słupku: w rządku pól, na który wskazuje strzałka, znajduje się umieszczona obok niej cyfra.
To i kilka podobnych zadań, które trafiły do „Omnibusa”, rodziło się w bólach i prawdopodobnie ich rozwiązywanie także będzie dla niektórych główkołamaczy „bolesne”, ale – mam nadzieję – pożyteczne.
A gościom Łamibloga proponuję dodatkowy znacznie twardszy orzech do zgryzienia.
Piątkę obok powyższego słupka można zastąpić inną cyfrą, a rozwiązanie nadal będzie tylko jedno. Jaka cyfra nadaje się na zastępczynię? Dodam, że możliwości są przynajmniej dwie.

Komentarze
Rozwiązanie słupka:
___14
x__74
______
___56
__98
______
_1036
Gdyby strzałka wskazująca teraz 5 zjechała rząd niżej, to mogłaby wskazywać:
a) 7
____97
x___11
_______
____97
___97
_______
__1067
b) 5
____19
x___54
_______
____76
___95
_______
__1026
Czy takie zjechanie strzałki niżej było dopuszczalne?
Czy koniecznie na jej poziomie trzeba było szukać czegoś unikatowego?
Strzałka nie może zmienić miejsca. Zmienić powinna się tylko cyfra obok niej.
mp
A co jest nie tak z mnożeniem 14 x 74?
Z tym mnożeniem oczywiście wszystko jest TAK. Uwolniłem je, bo to jest rozwiązanie zadania z Omnibusa, a nie twardszego orzecha ekstra.
mp
14 x 76, liczbę 5 można zastąpić 8 lub 4.
Pozdrawiam 🙂
Oprócz głównego rozwiązania z „5” w trzeciej linii:
14*74 56 98= 1036
mamy też układ z „4” w trzeciej linii:
14*76 84 98= 1064
oraz układ z „8” w trzeciej linii:
14*76 84 98= 1064
czyli „4” lub „8” są tu „jednoznaczne” dla jednego mnożenia.
Zgodnie ze wskazówką Autora mamy „co najmniej dwie możliwości” zastąpienia tej „5”-ki.
I jednocześnie „co najwyżej dwie” 😉
Zdaniem Autora jest jeszcze trzecia możliwość – 9-ka zamiast 5-ki.
Autor prosi o potwierdzenie, czy ma rację, czy nie.
mp
Rzuciłem kośćmi i wypadło mi 4 i 8 … bo to takie specjalne kości 😉
PS. Gdyby jednak pozostawić jedynkę i piątkę, to szóstkę obok powyższego słupka można zastąpić inną cyfrą, a rozwiązanie nadal będzie tylko jedno. Dodam, że możliwości są dwie 🙂
PS. Gdyby zaś jedynkę zastąpić dwójką, to piątkę można by zastąpić jedną cyfrą tak, aby rozwiązanie było jednoznaczne bez dodatkowych warunków (bez tego z szóstką).
Chyba byłem zbyt lakoniczny w kwestii podstawowej zagadki.
Dopiszę, że oba warunki zamienne dla „5” tj. „4” i „8” wskazują jednoznacznie na jedno działanie 14 x 76 (inne niż „5” – 14 x 74).
Dla „9-ka zamiast 5-ki”:
12*88 96 96= 1056
16*66 96 96= 1056
96*11 96 96= 1056
97*11 97 97= 1067
Jeśli czegoś nie przeoczam to są 4 rozwiązania.
Zgadza się. To ja przeoczam.
mp
Piątkę możemy zastąpić czwórką lub ósemką.
Byłam dziś w escape roomie. Jedno z zadań polegało na… uzupełnieniu liczbami szkieletu mnożenia pisemnego 🙂 Iloczyn okazał się kodem do kłódki. Dobry pomysł ktoś miał.
Cyfrę 5 możemy zastąpić 4 lub 8.
W obu przypadkach wyłowimy mnożenie 14X76.
Ale idąc dalej, rozważmy ogólny schemat w którym bierzemy szkielet z zadania a cyfry 1,5,8 zastąpmy przez a,b,c.
górny czynnik=gc
dolny czynnik=dc
górny iloczyn=i1
dolny iloczyn=i2
wynik=wynik
Otrzymujemy 86 zadań (układów cyfr: a,b,c) z jednoznacznym rozwiązaniem:
#,a,b,c, gc,dc, i1, i2, wynik
1,1,2,3,12,86,72,96,1032
2,1,2,8,14,72,28,98,1008
3,1,4,6,14,76,84,98,1064
4,1,5,3,14,74,56,98,1036
5,1,5,6,14,74,56,98,1036
6,1,5,7,19,53,57,95,1007
7,1,6,3,14,74,56,98,1036
8,1,6,4,16,64,64,96,1024
9,1,7,3,12,86,72,96,1032
10,1,7,5,14,75,70,98,1050
11,1,8,6,14,76,84,98,1064
12,2,2,3,24,43,72,96,1032
13,2,2,8,14,72,28,98,1008
14,2,4,3,47,22,94,94,1034
15,2,4,9,49,21,49,98,1029
16,2,7,3,24,43,72,96,1032
17,2,7,6,19,54,76,95,1026
18,2,8,7,49,22,98,98,1078
19,2,9,4,47,22,94,94,1034
20,2,9,7,49,22,98,98,1078
21,2,9,8,49,22,98,98,1078
22,2,9,9,49,21,49,98,1029
23,3,4,2,32,32,64,96,1024
24,3,5,1,14,74,56,98,1036
25,3,5,3,14,74,56,98,1036
26,3,5,6,14,74,56,98,1036
27,3,6,2,32,32,64,96,1024
28,3,6,3,14,74,56,98,1036
29,3,6,4,32,32,64,96,1024
30,3,9,5,32,33,96,96,1056
31,3,9,6,32,33,96,96,1056
32,3,9,8,33,33,99,99,1089
33,3,9,9,33,33,99,99,1089
34,4,2,3,24,43,72,96,1032
35,4,4,9,49,21,49,98,1029
36,4,7,1,24,43,72,96,1032
37,4,7,2,24,43,72,96,1032
38,4,7,3,24,43,72,96,1032
39,4,8,7,49,22,98,98,1078
40,4,9,7,49,22,98,98,1078
41,4,9,8,49,22,98,98,1078
42,4,9,9,49,21,49,98,1029
43,5,5,3,14,74,56,98,1036
44,5,5,6,14,74,56,98,1036
45,5,5,7,19,53,57,95,1007
46,5,6,2,19,54,76,95,1026
47,5,6,3,14,74,56,98,1036
48,5,7,2,19,54,76,95,1026
49,5,7,5,14,75,70,98,1050
50,5,7,6,19,54,76,95,1026
51,5,7,7,19,53,57,95,1007
52,6,4,6,14,76,84,98,1064
53,6,8,6,14,76,84,98,1064
54,6,9,7,97,11,97,97,1067
55,7,1,1,13,77,91,91,1001
56,7,2,8,14,72,28,98,1008
57,7,4,2,14,73,42,98,1022
58,7,4,4,14,76,84,98,1064
59,7,4,6,14,76,84,98,1064
60,7,5,1,14,74,56,98,1036
61,7,5,3,14,74,56,98,1036
62,7,5,6,14,74,56,98,1036
63,7,6,2,19,54,76,95,1026
64,7,6,3,14,74,56,98,1036
65,7,7,5,14,75,70,98,1050
66,7,8,4,14,76,84,98,1064
67,7,8,6,14,76,84,98,1064
68,7,9,6,97,11,97,97,1067
69,8,2,3,12,86,72,96,1032
70,8,2,8,14,72,28,98,1008
71,8,4,6,14,76,84,98,1064
72,8,4,8,12,84,48,96,1008
73,8,4,9,49,21,49,98,1029
74,8,5,1,14,74,56,98,1036
75,8,5,3,14,74,56,98,1036
76,8,5,6,14,74,56,98,1036
77,8,6,2,12,85,60,96,1020
78,8,6,3,14,74,56,98,1036
79,8,6,5,12,88,96,96,1056
80,8,7,2,12,86,72,96,1032
81,8,7,3,12,86,72,96,1032
82,8,7,5,14,75,70,98,1050
83,8,8,6,14,76,84,98,1064
84,8,9,2,49,21,49,98,1029
85,8,9,5,12,88,96,96,1056
86,8,9,6,12,88,96,96,1056