LCD cd.
Dawno nic mnie tak nie zaskoczyło, jak zaszarzenie 20 czarnych kresek przez Andrzeja111 w słupkowym mnożeniu sprzed tygodnia. Taka porcja „nadinformacji” rzadko się zdarza w łamigłówkach diagramowych. Inna sprawa, czy radykalne ograniczenie danych nie powoduje, że zadanie – mimo jednego rozwiązania – staje się rozrywką dla komputera, czyli ekstremalnie żmudną. Ocenę tego pozostawiam zainteresowanym, prezentując poniżej słupek LCD po „przejściach”.

Ciekawe wydaje się uogólnienie tego tematu, czyli: ile co najmniej szarych kresek należy zmienić w czarne (jest częścią cyfry) lub białe (nie jest częścią cyfry) w danym „szkielecie” mnożenia LCD, aby możliwe było jednoznaczne rozszyfrowanie działania?
Na przykład, w poniższym mnożeniu trzeba jedną szarą kreskę zaczernić i jedną zabielić tak, aby działanie z tak oznaczonymi dwoma modułami było tylko jedno – przy warunku, że każda cyfra w mnożeniu jest inna.
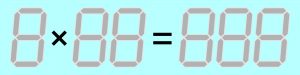
![]()

Komentarze
Niestety nie dysponowałem wystarczającą ilością czasu ani mocy obliczeniowej aby poznęcać się nad przykładem z poprzedniego wpisu. Wynik Andrzeja111 jest rzeczywiście zaskakujący, ale bardzo proszę mocno złapać się fotela/krzesła/biurka/*, bowiem:
w przedstawionym przykładzie udało mi się zaszarzyć kolejne 3 kreski, tak aby nie utracić jednoznaczności rozwiązania!
Kolejne kreski do usunięcia to:
– ostatnia kreska w cyfrze jedności w pierwszym rzędzie,
– ostatnia kreska w cyfrze dziesiątek w czwartym rzędzie,
– jedna z dwóch kresek (dowolna) w cyfrze dziesiątek w drugim rzędzie.
Zaszarzyłem wskazany tercet (w drugim rzędzie białą). Zostało 8 czarnych i 4 białe. Czy to koniec zaszarzania?
mp
Zabielamy szóstą kreskę w pierwszej cyfrze działania i zaczerniamy piątą kreskę w trzeciej cyfrze.
2 x 78 = 156
Bez kresek różnych rozwiązań tego zadania jest 76. Tylko dwa mają „2” na drugim miejscu w iloczynie. A dwójka jest jedyną, która nie ma prawej dolnej pionowej kreski.
1) 7×89=623
2) 5×64=320
W obu przypadkach białą kreską zaznaczamy prawą dolną pionową kreskę w „2”.
Czarną w obu przypadkach można ustawić różnie. Np.:
1) w „7” prawą górną
2) w „5” lewą górną
W obu przykładach można zaznaczyć dwie białe kreski i też będzie jedno rozwiązanie .
1) w „6” prawą górną pionową
2) w „4” dolną (górną) poziomą
Czy może być tak?
http://pokazywarka.pl/rr80zg/
Oczywiście: 8*79=632. To jedno z możliwych rozwiązań.
mp
Mam taki pomysł: cyfrę 2 wskazujemy jednoznacznie przez pobielenie pionowej kreski u dołu po prawej stronie. Z kolei kreskę czarną pionową u dołu po lewej stronie mają tylko 2, 6 i 8. Skoro 2 nie może być, to zostają do rozważenia 6 i 8. I wychodzą takie przykłady:
http://pokazywarka.pl/2znvax/
2*93=186 i 2*54=108
3*54=162 i 6*97=582
Pozostałe OK i pomysł jak należy.
mp
A to jest oparte na pomyśle, że 1 i 4 nie mają górnej kreski. Jeśli 1 na jakiejś pozycji jest niemożliwe, to brak górnej kreski jednoznacznie wskazuje na 4. Czarna kreska wskazuje na 2, 6 lub 8.
http://pokazywarka.pl/w1t79i/
Pomysł jeszcze lepszy, bo bez jednoznacznej dwójki z białą kreską.
mp
Jeśli chodzi o nowe zadanie, to wystarczą trzy białe kreski, jakkolwiek to nie zabrzmi. Tutaj duże znaczenie ma fakt, że biała pionowa kreska po prawej na dole jednoznacznie identyfikuje dwójkę. Jeśli więc takie kreski postawimy w dwóch ostatnich cyfrach wyniku i jeszcze dodamy poziomą białą kreskę na daszku pierwszej cyfry (co z kolei pozwala wpisać tylko 1 lub 4), od razu otrzymujemy wynik: 1×22=022.
Jeśli zmienimy warunki zadania i wykluczymy białe kreski, to potrzebujemy pięciu czarnych kresek: https://snag.gy/HGrhVy.jpg
Jeśli nie pozwolimy, aby liczba (dwu- lub trzycyfrowa) rozpoczynała się zerem, to: https://snag.gy/H7drfP.jpg
I jeszcze jedno z jedną białą kreską: https://snag.gy/t06aPJ.jpg
W poprzednim komentarzu odniosłem się do nowego zadania, ale teraz się zastanawiam, co dokładnie jest nowym zadaniem, bo chyba jednak źle zrozumiałem 🙂
Przy warunku na to, by każda cyfra była inna: https://snag.gy/7rbhGT.jpg
A rozwiązaniem jest: 5*64=320
Tutaj algorytm dla ciekawych: https://dotnetfiddle.net/GMUJGy
Algorytm raczej polegnie w poprzednim zadaniu, choć jeszcze nie sprawdzałem.
A jakby tak się umówić, że dwie białe kreski to mniej niż jedna biała i jedna czarna? Byłoby nowe minimum:
http://pokazywarka.pl/vp5lnc/
Poprzednio dwa razy wysłałam ten sam przykład: 4*27=108
Ten drugi miał być oznaczony inaczej:
4 – biała górna kreska
2 – biała pionowa dolna kreska
Mam też kolejne minimum: nie zaznaczamy żadnych kresek, tylko uzupełniamy zdanie: „każda cyfra w mnożeniu jest inna” o informację: „i wszystkie cyfry tworzą ciąg arytmetyczny”. Tylko że wtedy zrobiło nam się trochę inne zadanie… 🙂
Po 7 godzinach pracy (dokładnie po 411 minutach) i sprawdzeniu na siłę wszystkich możliwości, komputer orzekł że:
– zostawiając maksymalnie 10 nieszarych kresek zadanie zawsze ma przynajmniej 2 rozwiązania.
– istnieje 78 układów 11 kresek, dla których zadanie ma unikalne rozwiązanie.
Prezentuję dwa przykładowe układy, jeden zawiera 9 czarnych i 2 białe kreski, drugi 7 czarnych i 4 białe:
http://pokazywarka.pl/u8om2p/
Właśnie odebrałam miłą przesyłkę – grę Rachmistrz. Serdecznie dziękuję! 🙂
Przyjemnego rachowania 🙂
mp
Czy zakładamy że cyfry znaczące (pierwsze z lewej) są > 0 ?
Tak
mp
Brawo miodziu !
Niestety miałem inne priorytety i nie mogę się pochwalić takim wynikiem. (Z drugiej strony przestraszająca była ilość kombinacji do sprawdzenia – właściwie to jestem zdziwiony, że tych 411 minut wystarczyło…)
W kwestii układów „jednoznacznych”:
Intuicyjnie zakładałem, że większość nieszarych kresek znajdzie się w mnożnej i mnożniku – czyli w pierwszej i drugiej linii – tak jest w jednym z przykładów.
Czy taka zależność występuje w całej populacji rozwiązań?
Te 11 kresek jest potrzebnych w wypadku mnożenia 138×898. Można sobie z łatwością jednak wyobrazić inne 3-cyfrowe liczby do przemnożenia, gdzie wystarczy 6 kresek. I teraz ciekawe, czy da się zejść poniżej 6. Myślę, że tak.
1) Oznaczenia. Można czytelnie zakodować 7 kresek 1-cyfrowego wyświetlacza w postaci:
GS
GL GP
SS
DL DP
DS
Dalej skorzystam z tego, tylko dwójkę wyróżnia biała DP.
Kolejne cyfry działania możemy oznaczyć kolejnymi literami:
a * bc = def
2) Wśród dopuszczalnych działań są tylko dwa mnożenia ze środkową cyfrą iloczynu (e) równą 2:
a) 5*64=320
b) 7*89=623
Każde z nich możemy zaszyfrować przy pomocy tylko dwóch kresek w cyfrach iloczynu:
a) środkowa (e): biała DP / ostatnia (f): czarna GL
b) środkowa (e): biała DP / ostatnia (f): czarna SS
@apartado
Dziekuje.
Mozliwych ukladow do sprawdzenia bylo 11 z 35, czyli niecale 418 mln. W każdym z nich do sprawdzenia około 65 tys możliwych rozwiązań, co daje ok. 20 bln możliwości, ale trzeba pamiętać, że gdy dla danego układu 11 kresek znajdziemy choć jedno rozwiązanie inne od docelowego, to dalsze sprawdzanie można przerwać bez sprawdzania tych wszystkich 65 tysmożliwości.Poza tym kreski pozostawione w czynnikach od razu znaiczbęych rozwiązań. Załóżmy, że to zmniejsza te liczbę z 65 tys do 6,5 tys., czyli te 20 bln przypadków do 2 bln.
Program działał 411 minut, czyli ok. 25 tys sekuekund na obrobienie 2 bln operacji daje ok. 100 mln operacji na sekunde, co wydaje sie osiągalne dla zwykłego procesora.
Co do rozkładu pozostawoanych kresek pomiędzy czynniki i pozostałe liczby, to o ile pamiętam byl on dość rownomierny. Dane mam zapisane na komputerze w pracy, po Nowym Roku obiecuje je przejrzec i odpowiedzieć dokładniej na pytanie.
@ OlaGM
Twój problem również wydaje sie ciekawy do sprawdzenia. Wrócę do niego po Nowym Roku.
@wszyscy miłośnicy łamania (swojej) głowy
Wesołych, zdrowych i spokojnych świąt Bożego Narodzenia!
Przyłączam się do życzeń.
mp
Siedzę sobie właśnie nad kartką, bo komputera o tej porze włączać nie wypada 🙂 Mnożenie pisemne dwóch liczb 3-cyfrowych ze wskazaniem 5 kresek już wymyśliłam. Jutro między pieczeniem makowca i jabłecznika spróbuję zejść do 4.
Wesołych Świąt 🙂
@miodziu
Jakoś (pośpiech!) zrozumiałem, że w wyniku Twoich działań mamy wyselekcjonowane konkretne czynniki, dla których ilości kresek są minimalne.
Wątek z @OlaGM uświadomił mi, że to jest rozwiązanie dla tylko jednego mnożenia z zadania.
Moja ocena złożoności obliczeniowej zakładała, że należy sprawdzić wszystkie kombinacje kresek, dla wszystkich położeń w „szkielecie” mnożenia.
Liczba takich kombinacji wyszła mi osiemnastocyfrowa – i to dla jednego zestawu typu 5 białych + 5 czarnych;
a takich układów jest sporo więcej: sześć kresek „domniemywanych” przez @OlaGM to może być na przykład 2 czarne + 4 białe.
podsumowując:
Moje „Brawo” pozostaje aktualne – chociaż w trochę innej konkurencji 😉
A przy okazji życzę Wszystkim Miłych Świąt
Czasem wystarczą 3 kreski. Mój 12-letni syn to rozwiązał 🙂
http://pokazywarka.pl/2dc1gc/
@OlaGM
Olu, w siatce którą podałaś brakuje jednego iloczynu pośredniego. Ale załóżmy, że siatka jest w porządku (jeśli chodzi o ilości pól).
Przy podanym przez Ciebie układzie białych kresek nie może istnieć żadne rozwiązanie gdyż pierwszy i trzeci iloczyn muszą być równe a nie mogą bo pierwszy ma trzy cyfry a drugi cztery.
@everybody
Ponieważ prawa, dolna, biała kreska jednoznacznie identyfikuje cyfrę 2, to narzuca się zbadanie siatki z minimalną ilością tych właśnie białych kresek.
Dalej, zamiast: „prawa, dolna, biała kreska” mówimy po prostu: „dwójka”.
W konkurencji „dwójki tylko nad pierwszą kreską” – nie ma rozwiązań.
W konkurencji: „dwójki tylko poza czynnikami” tzn. wymuszamy „dwójki” dopiero pod pierwszą kreską), komputer wyrzucił mi właśnie dwie takie siatki, każda ma 4 „dwójki”.
Obie siatki mają 3 „dwójki” w pierwszym iloczynie (pod pierwszą kreską) oraz czwartą „dwójkę” odpowiednio na 3 i 4 miejscu wyniku (pod drugą kreską).
Jeśli się nie pomyliłem to mniej niż 4 białe kreski się nie da (w konkurencji: „tylko białe kreski ale poza czynnikami” tzn. wymuszamy „dwójki” dopiero pod pierwszą kreską).
Liczymy dalej pozostałe siatki dla czterech białych kresek poza czynnikami …
Komputer znalazł jeszcze 29 układów 4 „dwójek” pod pierwszą kreską i na pewno jeszcze by coś znalazł ale mu przerwałem, gdyż czekają już nowe wyzwania.
@Spytko
Sęk w tym, że nie brakuje tego rzędu. Jego po prostu nie ma. Jeśli w trakcie mnożenia pisemnego przyjdzie nam mnożyć przez 0, to tego nie robimy. Informacja, że mój syn to rozwiązał, oprócz tego, że chciałam się pochwalić, jakie to zdolne dziecko wydałam na świat, miała i takie znaczenie: rób jak uczeń w szkole.
Pozdrawiam 🙂
@Spytko
Piszesz, że pierwszy i trzeci Iloczyn muszą być równe. No przecież są.
496 x 202 = 100192 to jedyne rozwiązanie, jestem o tym przekonana. Nie wiem, co liczył ten komputer 🙂
@OlaGM
Rozumiem, że zajmujemy się szkieletem z zadania wyjściowego.
Trzeci iloczyn pośredni (nad drugą kreską) ma być liczbą czterocyfrową,
więc jego pierwsza cyfra musi być różna od zera. U Ciebie pierwszej cyfry nie ma.
Nie możemy przyjąć, że tam dopisujemy sobie zero bo w ten sposób 2X2=4 też wpasujemy w tą siatkę.
Środkowy iloczyn pośredni (który pominęłaś) powinien składać się z trzech zer i znowu brak nam czwartej cyfry z przodu.
Nie możemy przyjąć, że jest tam zero bo mielibyśmy dwa rodzaje zer.
Jedne z działań arytmetycznych a drugie z dopisywania w miarę potrzeb.
Spójrz na zadanie z 14 grudnia. We wpisie nr 192347 z dumą podaję „drugie” rozwiązanie zadania, którego „nikt nie zauważył”.
Ale po chwili zauważyłem, że pierwszy iloczyn pośredni wystaje poza szkielet z zadania i odwołałem to „rozwiązanie”.
To był ten sam błąd tylko w drugą stronę. Ja miałem za dużo cyfr w stosunku do szkieletu a Ty masz ich za mało 🙂
Pani Olu, ja też nie rozumiem, o co chodzi Spytce (czy ktoś rozumie i zgadza się z powyższym wywodem?).
Moim zdaniem Pani zadanie jest pomysłowe, fajne i proste.
mp
@Spytko
A jak Ty zrobiłbyś szkielet do 496 x 202?
@OlaGM
Mój wywód odnosi się do następującego problemu:
Znaleźć minimalny układ kresek dający jedno jedyne rozwiązanie na szkielecie z zadania z dn. 20.12.2017
Jeśli tak to 2*496=992. 992 jest liczbą trzycyfrową a w szkielecie dla pierwszej „dwójki” mamy rzeczywiście format trzycyfrowy (dla iloczynu 2*496=992) ale dla drugiej „dwójki” mamy format czterocyfrowy.
Z reguły w takich sytuacjach przyjmuje się, że tą pierwszą cyfrą musi być coś z przedziału 1..9. A w zadaniu Oli zostaje tam puste miejsce.
Nieporozumienie może wynikać z tego, że rozmawiamy o różnych szkieletach. Ja o jednym, konkretnym a Wy o dowolnym 🙂
Mnie cały czas chodziło o znalezienie minimalnego układu kresek na tym jednym danym szkielecie z zadania. I tu chyba był pies pogrzebany 😉
Nie rozumiem „parcia” na 4-cyfrowy iloczyn cząstkowy dla drugiej dwójki, skoro w mnożeniu (rozwiązaniu) są tam 3 cyfry.
Przecież zadanie powstaje tak, że zwykłe cyfry w słupkowym zapisie mnożenia zastępuje się kreskowymi, a następnie wyklucza się niektóre kreski. A trudno zastąpić i wykluczyć coś, czego nie ma.
mp
@Spytko
Nie było moim zamiarem wpasowywanie się w tamten szkielet 🙂 Postawiłam przed sobą nieco inne zadanie: wymyślić takie mnożenie dwóch liczb 3-cyfrowych, dla których będzie można podać jak najmniejszą liczbę kresek. I dobrałam liczby tak, że wystarczyły tylko 3 kreski. Resztę informacji należało pozyskać na podstawie liczby cyfr w poszczególnych liczbach.
Jeśli natomiast chodzi o problem: jaka jest minimalna liczba kresek dla poprzedniego schematu, to potrafię podać przykład dla 4 kresek. Być może to jest właśnie minimum…
Pozdrawiam, Ola
@Spytko z Melsztyna
OlaGM w komentarzu z 23 grudnia 11:24 napisała tak:
„Te 11 kresek jest potrzebnych w wypadku mnożenia 138×898. Można sobie z łatwością jednak wyobrazić inne 3-cyfrowe liczby do przemnożenia, gdzie wystarczy 6 kresek. I teraz ciekawe, czy da się zejść poniżej 6. Myślę, że tak.”
W postawionym przez Olę zadaniu nie ma mowy o żadnym szkielecie. Ola stawia problem tak:
„Ciekawe, czy istnieje jakiś iloczyn dwóch trzycyfrowych liczb, dla których w szkielecie mnożenia (poprawnym, dla tych konkretnych trzycyfrowych liczb) wystarczy ujawnić tylko 6 kresek, aby rozwiązanie było jednoznaczne”.
Później pojawia się przykład, w którym wystarczą tylko 3 kreski.
Nieporozumienie wynika z tego, że Ty cały czas zakładasz, że postawiony problem odnosi się do schematu z niniejszego wpisu na blogu – a tak nie jest – problem został postawiony ogólnie.
@wszyscy
Sam szkielet do mnożenia trzycyfrowych liczb bardzo dużo mówi nam o liczbach które mnożymy – w szczególności brak jakiegoś wiersza oznacza, że w drugim czynniku na odpowiedniej pozycji musi być cyfra 0. Jest to bardzo znacząca informacja, mimo iż w samym szkielecie nie używamy żadnej kreski (których liczbę chcemy zminimalizować), to znacznie ogranicza liczbę rozwiązań.
W schemacie z 20 grudnia wystarczy podać 3 kreski, żeby dostać jednoznaczne rozwiązanie, donoszę uprzejmie 🙂
Z czterema kreskami:
http://pokazywarka.pl/kwdsws/
Z trzema kreskami:
http://pokazywarka.pl/lqth8m/
Brawo OlaGM!!!
Sprawdzę te układy – sprawdzić jest mi programem łatwo (o wiele gorzej ze znajdowaniem…), ale teraz nie mam za bardzo czasu, więc dopiero w weekend.
Dzięki, Apartado 🙂
A jednak nie, niestety. Trzy kreski to za mało, czwarta jest niezbędna. W każdym z przykładów z trzema kreskami trzeba dodać jeszcze jedną, określając trzecią cyfrę mnożnika jako 2.
@OlaGM
Nieporozumienie w sprawie szkieletu wyjaśnione 🙂
Jeśli chodzi o Twój wpis 192410 z 10 stycznia 2018, w części dotyczącej układów z 4 kreskami to sprawdziłem, że wszystkie mają jednoznaczne rozwiązania:
rys. 1) 112,992
rys. 2) 112,992
rys. 3) 122,992
rys. 5 – ten z wątpliwościami) 772,521
Jeśli chodzi o rozwiązania tylko z trzema dwójkami to program przeszukał mi już część przestrzeni nic nie znajdując ale skoro temat cały czas żyje to puszczam go by sprawdził resztę terenu 🙂
Cześć, Spytko 🙂
Te przykłady z 3 kreskami niestety wyrzucą na pewno mnóstwo rozwiązań…
Dlatego dokładam czwartą kreskę: http://pokazywarka.pl/y6uirl/
Ogólnie pomysł na to miałam taki:
– wezmę mnożną z zakresu 112-124 (po to, żeby mnożnik musiał mieć dwie pierwsze cyfry 99 i żeby nic innego nie było możliwe)
– jako trzecią cyfrę mnożnika wezmę 2
– podam od razu wynik mnożenia mnożnej przez 2 (który to wynik będzie na tyle niski, że nie da się go zinterpretować jako „3 x coś-tam”, „4 x coś tam” itd.)
No i fakt – na tyle niski był. Ale nie wzięłam pod uwagę, że można go zinterpretować jako „1 x”. To znaczy: wzięłam, ale jakąś dobę później…
Łamigłówka fascynująca. Dawno nic mnie tak nie wciągnęło 🙂
Olu, trzy kreski rzeczywiście dają wiele rozwiązań.
Za to ostatnie Twoje przykłady z wpisu 192419 są już perfekcyjne 🙂
rys. 1) 112*992
rys. 2) 113*992
rys. 3) 121*992
rys. 4) 122*992
rys. 5) 123*992
Sprawdziłem też wszystkie kombinacje trzech dwójek na tym szkielecie i niestety nie ma żadnego, jednoznacznego rozwiązania.
Nasz szkielet to:
ABC
DEF
——-
GHI
IJKL
ŁMNO
———-
PRSTUW
Można jednoznacznie dwiema kreskami pokazać, czym są Ł i P. Te dwie cyfry albo są sobie równe, albo różnią się o 1. Jeśli np. Ł nie ma górnej poziomej kreski, a P – nie ma pionowej górnej prawej, to identyfikuje je jako 4 i 5. I teraz pytanie, czy układ z 4 i 5 w tym miejscu ma gdzieś jakąś cyfrę tylko w jednym wypadku. Na przykład 2…
@apartado:
Pytałeś o rozkład wyników. Nie mam siły ich analizować, dlatego przesyłam je w całości.
Notacja:
– wszystkie cyfry w szkielecie mnożenia porządkujemy od góry do dołu, a w ramach tego samego wiersza od lewej do prawej
– w ramach poszczególnych cyfr numerujemy poszczególne fragmenty wyświetlacza w identyczny sposób, tzn. pierwszy jest górny, potem górny lewy, górny prawy, centralny, dolny lewy, dolny prawi i dolny.
W tak utworzonym ciągu uwzględniamy tylko nieszare pozycje z diagramu oryginalnego problemu.
W poniższym zapisie jeden wiersz oznacza jedno rozwiązanie.
W każdym wierszu pozycja oznaczona liczą 0 oznacza, że w diagramie dana NIESZARA kreska powinna zostać wyszarzona. Pozostałe 11 niewyszarzonych kresek stanowi diagram – który posiada dokładnie 11 nieszarych kresek, którego rozwiązanie jest jednoznaczne.
00100000000000010010000111100101011
00110000000000010010000100011101011
00110000000000010010000100011101101
00110000000000010010100100010101101
00110000000000110010000100011101010
00110000000000110010000100011101100
00110000000000110010000100101101010
00110000000000110010000100101101100
01010000000000110010010000100101110
01010000000000110010010000101101010
01010000000000110010010000101101100
01010000000000110010100000100101110
01010000000000110010100000101101010
01010000000000110010100000101101100
01010010000000110010000000100101110
01010010000000110010000000101101010
01010010000000110010000000101101100
01100000000000010010000010110101011
01100000000000010010000011100101011
01100000000000110010000010110101010
01100000000000110010000011100101010
01110000000000010010000000010101111
01110000000000010010000000011101011
01110000000000010010000000011101101
01110000000000010010000010010101011
01110000000000010010010000010101011
01110000000000010010010001000101011
01110000000000110010000000000111110
01110000000000110010000000001111010
01110000000000110010000000001111100
01110000000000110010000000010101110
01110000000000110010000000010111100
01110000000000110010000000011101010
01110000000000110010000000011101100
01110000000000110010000000100101110
01110000000000110010000000101101010
01110000000000110010000000101101100
01110000000000110010000010010101010
01110000000000110010000010010101100
01110000000000110010001000000101110
01110000000000110010001000001101010
01110000000000110010001000001101100
01110000000000110010001000010101100
01110000000000110010010000000101110
01110000000000110010010000000111100
01110000000000110010010000001101010
01110000000000110010010000001101100
01110000000000110010010000001111000
01110000000000110010010000010101010
01110000000000110010010000010111000
01110000000000110010010001000101010
01110000000000110010010001000111000
01110000000000110010010010000101100
01110000000000110010010100000101010
01110000000000110010010100000111000
01110000000000110010011000000101100
01110000000000110010011000010101000
01110000000000110010100000010101100
01110000000000110010110000000101100
01110000000000110010110000001101000
01110000000000110010110000010101000
01110000000000110010110001000101000
01110000000000110010110100000101000
01110000000010010010000000010101101
01110000000010110010000000000111100
01110000000010110010000000010101100
01110000000010110010000000100101100
01110000000010110010001000000101100
01110000000010110010010000000101010
01110000000010110010010000000101100
01110000000010110010010000000111000
01110000000010110010110000000101000
01110000000100010010000000010101011
01110000000100110010000000010101010
01110000100000110010000000000101110
01110000100000110010000000001101010
01110000100000110010000000001101100
01110000100010110010000000000101100
@ miodziu
Dziękuję za to „wypracowanie”.
Dane pokazują, że nieszare kreski są potrzebne raczej w końcowych liniach działania – sporo początkowych można usuwać).
To by sugerowało, że moja intuicja w tym zakresie mnie zawiodła, ale w tzw. międzyczasie OlaGM pokazała, że wystarczają cztery kreski (Jej rozwiązania mają nieszare kreski raczej na początku).
Czyli tu bardziej w zgodzie z intuicją.
Przy okazji:
@ OlaGM
Szukałem takiego położenia 2-ki (dla Ł=4, P=5), żeby była ona trzecią z kresek – nie znalazłem takiego jednoznacznego układu.
@apartado
A ja starałam się szukać dla Ł=1 i P=1, ale przerwałam, bo nie bardzo wierzyłam w powodzenie.
Pozdrawiam 🙂
@Ola
Szkielet mnożenia tworzy 161 kresek.
Teraz, kiedy wiemy, że rozwiązanie to 4 lub mniej kresek, nie powinno być problemu ze sprawdzeniem wszystkich kombinacji:
3 kreski spośród 161 można wybrać na 682640 sposobów.
Biorąc pod uwagę różne nieszarości (białe lub czarne) ilość ta wzrasta siedmiokrotnie.
Czyli mamy 4778480 kombinacji do sprawdzenia.
Jeśli uśmiechniemy się ładnie @miodziu, to problem mamy z głowy 🙂
@apartado
Miodziu ostatnio cierpi na ZZZiR(*) i pierwsze o czym myśli w chwili wolnej to SiO(*).
Szczerze mówiąc zgubiłem się w tej dyskusji i nie wiem jak jest postawiony problem.
Bardzo zatem proszę, aby ktoś w jednym wpisie jasno określił problem do rozwiazania. Ja potraktuje to jako „ładne usmiechniecie sie” i będę pamiętał, aby kiedyś do tego problemu wrócić.
Legenda (*):
– ZZZiR – zespół zmęczenia zawodowego i rodzinnego
SiO – sen i odpoczynek
@miodziu
Problem postawiony jest tak: czy można znaleźć w szkielecie z 20 grudnia takie 3 kreski do zaznaczenia, które dadzą jednoznaczne rozwiązanie?