Nadzadanie

To jest zadanie przede wszystkim dla wszystkich tych, którzy łamigłówkę sprzed tygodnia uznali za łatwą. Rodzaj zadania jest taki sam, czyli:
Do kratek w każdej działce należy wpisać n różnych cyfr – od 1 do n, gdzie n jest liczbą kratek tworzących daną działkę. W całym diagramie w sąsiednich kratkach – stykających się bokiem lub tylko rogiem – nie mogą znaleźć się jednakowe cyfry.

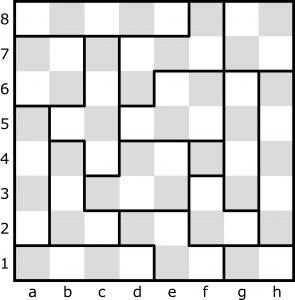
Rozwiązań jest więcej niż jedno, ale to tylko podzadanie. Natomiast zadanie główne, czyli „nadzadanie”, zawarte jest w pytaniu:
jaką jedną liczbę i do której kratki należy wpisać, aby rozwiązanie było tylko jedno?
Czy nadzadanie ma jedno rozwiązanie? Moim zdaniem kratka jest jedna, ale liczby w nią wstawiane mogą być dwie. Czy mam rację?

Komentarze

[OlaGM]

> Moim zdaniem kratka jest jedna, ale liczby w nią wstawiane
> mogą być dwie.
Doszłam do innego wniosku: kratki są dwie, a liczba ta sama.
Wstawienie 3 w polu 7d albo w polu 8b daje jednoznaczne rozwiązanie:
23145131
14232424
23151313
15424524
42313131
31524242
24313135
31242421

[Antyp1958]

To są wszystkie rozwiązania podstawowego zadania.
2 3 1 4 5 1 3 1
1 4 2 3 2 4 2 4
2 3 1 5 1 3 1 3
1 5 4 2 4 5 2 4
4 2 3 1 3 1 3 1
3 1 5 2 4 2 4 2
2 4 3 1 3 1 3 5
3 1 2 4 2 4 2 1
—————
2 4 1 5 3 1 3 1
1 3 2 4 2 5 2 4
2 4 1 3 1 3 1 3
1 3 5 2 4 5 2 4
4 2 4 1 3 1 3 1
3 1 5 2 4 2 4 2
2 4 3 1 3 1 3 5
3 1 2 4 2 4 2 1
—————
2 4 1 5 3 1 3 1
1 3 2 4 2 5 2 4
2 4 1 3 1 3 1 3
1 3 5 2 5 4 2 4
4 2 4 1 3 1 3 1
3 1 5 2 4 2 4 2
2 4 3 1 3 1 3 5
3 1 2 4 2 4 2 1
—————
2 4 1 5 3 1 3 1
1 3 2 4 2 5 4 2
2 4 1 3 1 3 1 3
1 3 5 2 4 5 2 4
4 2 4 1 3 1 3 1
3 1 5 2 4 2 4 2
2 4 3 1 3 1 3 5
3 1 2 4 2 4 2 1
—————
2 4 1 5 3 1 3 1
1 3 2 4 2 5 4 2
2 4 1 3 1 3 1 3
1 3 5 2 5 4 2 4
4 2 4 1 3 1 3 1
3 1 5 2 4 2 4 2
2 4 3 1 3 1 3 5
3 1 2 4 2 4 2 1
—————
2 4 5 1 3 1 3 1
1 3 2 4 2 5 2 4
2 4 1 3 1 3 1 3
1 3 5 2 4 5 2 4
4 2 4 1 3 1 3 1
3 1 5 2 4 2 4 2
2 4 3 1 3 1 3 5
3 1 2 4 2 4 2 1
—————
2 4 5 1 3 1 3 1
1 3 2 4 2 5 2 4
2 4 1 3 1 3 1 3
1 3 5 2 5 4 2 4
4 2 4 1 3 1 3 1
3 1 5 2 4 2 4 2
2 4 3 1 3 1 3 5
3 1 2 4 2 4 2 1
—————
2 4 5 1 3 1 3 1
1 3 2 4 2 5 4 2
2 4 1 3 1 3 1 3
1 3 5 2 4 5 2 4
4 2 4 1 3 1 3 1
3 1 5 2 4 2 4 2
2 4 3 1 3 1 3 5
3 1 2 4 2 4 2 1
—————
2 4 5 1 3 1 3 1
1 3 2 4 2 5 4 2
2 4 1 3 1 3 1 3
1 3 5 2 5 4 2 4
4 2 4 1 3 1 3 1
3 1 5 2 4 2 4 2
2 4 3 1 3 1 3 5
3 1 2 4 2 4 2 1
—————
2 4 5 1 3 1 3 1
1 3 2 4 5 2 4 2
2 4 1 3 1 3 1 3
1 3 5 2 4 5 2 4
4 2 4 1 3 1 3 1
3 1 5 2 4 2 4 2
2 4 3 1 3 1 3 5
3 1 2 4 2 4 2 1
—————
2 4 5 1 3 1 3 1
1 3 2 4 5 2 4 2
2 4 1 3 1 3 1 3
1 3 5 2 5 4 2 4
4 2 4 1 3 1 3 1
3 1 5 2 4 2 4 2
2 4 3 1 3 1 3 5
3 1 2 4 2 4 2 1
—————
2 5 1 4 3 1 3 1
1 3 2 5 2 4 2 4
2 4 1 3 1 3 1 3
1 3 5 2 4 5 2 4
4 2 4 1 3 1 3 1
3 1 5 2 4 2 4 2
2 4 3 1 3 1 3 5
3 1 2 4 2 4 2 1
—————
2 5 1 4 3 1 3 1
1 3 2 5 2 4 2 4
2 4 1 3 1 3 1 3
1 3 5 2 5 4 2 4
4 2 4 1 3 1 3 1
3 1 5 2 4 2 4 2
2 4 3 1 3 1 3 5
3 1 2 4 2 4 2 1
—————
2 5 1 4 3 1 3 1
1 4 2 5 2 4 2 4
2 3 1 3 1 3 1 3
1 5 4 2 4 5 2 4
4 2 3 1 3 1 3 1
3 1 5 2 4 2 4 2
2 4 3 1 3 1 3 5
3 1 2 4 2 4 2 1
—————
2 5 1 4 3 1 3 1
1 4 2 5 2 4 2 4
2 3 1 3 1 3 1 3
1 5 4 2 5 4 2 4
4 2 3 1 3 1 3 1
3 1 5 2 4 2 4 2
2 4 3 1 3 1 3 5
3 1 2 4 2 4 2 1
—————
2 5 1 4 3 1 3 1
1 4 2 5 2 4 2 4
2 3 1 3 1 3 1 3
1 5 4 5 2 4 2 4
4 2 3 1 3 1 3 1
3 1 5 2 4 2 4 2
2 4 3 1 3 1 3 5
3 1 2 4 2 4 2 1
—————
2 5 4 1 3 1 3 1
1 3 2 5 2 4 2 4
2 4 1 3 1 3 1 3
1 3 5 2 4 5 2 4
4 2 4 1 3 1 3 1
3 1 5 2 4 2 4 2
2 4 3 1 3 1 3 5
3 1 2 4 2 4 2 1
—————
2 5 4 1 3 1 3 1
1 3 2 5 2 4 2 4
2 4 1 3 1 3 1 3
1 3 5 2 5 4 2 4
4 2 4 1 3 1 3 1
3 1 5 2 4 2 4 2
2 4 3 1 3 1 3 5
3 1 2 4 2 4 2 1
—————
2 5 4 1 3 1 3 1
1 3 2 5 4 2 4 2
2 4 1 3 1 3 1 3
1 3 5 2 4 5 2 4
4 2 4 1 3 1 3 1
3 1 5 2 4 2 4 2
2 4 3 1 3 1 3 5
3 1 2 4 2 4 2 1
—————
2 5 4 1 3 1 3 1
1 3 2 5 4 2 4 2
2 4 1 3 1 3 1 3
1 3 5 2 5 4 2 4
4 2 4 1 3 1 3 1
3 1 5 2 4 2 4 2
2 4 3 1 3 1 3 5
3 1 2 4 2 4 2 1
Nadzadanie:
Teza nadzadania fałszywą jest (Yoda).
Przykład: w 8b należy wpisać 3 albo w 8e -5 wówczas jedyne rozwiązanie

2 3 1 4 5 1 3 1
1 4 2 3 2 4 2 4
2 3 1 5 1 3 1 3
1 5 4 2 4 5 2 4
4 2 3 1 3 1 3 1
3 1 5 2 4 2 4 2
2 4 3 1 3 1 3 5
3 1 2 4 2 4 2 1

[y-b]

Bez dodatkowych podpowiedzi można wypełnić planszę tak:

2xxxx131
1x2xxxxx
2x1x1313
1xxxxx24
42×13131
31524242
24313135
31242421

Brakujące miejsca udało mi się wypełnić na 20 sposobów. Kolejno rzędami będzie to:
314543242435542453 (1)
415334252443352454
415334252443352544
415334254243352454
415334254243352544
451334252443352454
451334252443352544
451334254243352454
451334254243352544
451334524243352454
451334524243352544
514335242443352454
514335242443352544
514345242433542453
514345242433542543
514345242433545243 (2)
541335242443352454
541335242443352544
541335424243352454
541335424243352544

Teraz sprawdzam, w której kolumnie jest jakaś cyfra występująca wyłącznie w jednym wierszu. Np. w pierwszej kolumnie jest to 3, a ta kolumna odpowiada polu B8.
B8:3, E8:5, D7:3, D6:5 (rozwiązanie (1))
D5:5, E5:2 (rozwiązanie (2))

Z tego wynikałoby, że jest sześć kratek, a w każdej tylko jedna możliwa cyfra. Ale historia z poprzedniego zadania uczy pokory 😉 Tam się pomyliłem w momencie, gdy pomylić się nie miałem prawa. A tutaj jest tyle cyferek, że prawo do pomyłki sobie daję. Jak czas pozwoli, zweryfikuję się programistycznie.

[logi]

Rozwiązanie:
23145131
14232424
23151313
15424524
42313131
31524242
24313135
31242421
można uzyskać wpisując na początku albo 3 w pierwszym rzędzie, drugiej kolumnie, albo 5 w pierwszym rzędzie piątej kolumnie, albo 3 w drugim rzędzie czwartej kolumnie, albo 5 w trzecim rzędzie czwartej kolumnie.

[y-b]

Potwierdziłem programem swoje poprzednie wyniki.

[kroQ]

Mi wyszło, że należy wpisać 5 na pole d6. Zacząłem kolorem czerwonym, po wpisaniu 5 kontynuowałem niebieskim.
https://image.prntscr.com/image/qn7gHJqkSMynrFRNR4gdNQ.png

[Michał S]

Jeżeli do kratki e8 wpisać 5 – to zadanie ma jedno rozwiązanie. Ale wpisanie tam cyfry 3 daje kilkanaście (15?) rozwiązań.

[Spytko z Melsztyna]

Nie tak szybko jak poprzednie zadanie ale dość łatwo idzie ręcznie.
Plansza wypełnia się bez rozgałęzień do pewnego stanu,
po czym możliwe są rozgałęzienia dające w sumie 20 rozwiązań.

Są 4 sprzęgnięte logicznie pola: (b8=d7=x) (e8=d6=y).
Przyjęcie x=3 ( y=5) pozwala uzyskać jednoznaczne rozwiązanie

23145131
14232424
23151313
15424524
42313131
31524242
24313135
31242421

Pozostałe, możliwe pary (x,y) dają:
(5,3) => 9 rozwiązania
(4,3) => 10 rozwiązań

[Spytko z Melsztyna]

@y-b:
Rzeczywiście (d5,e5)=(5,2) też daje jednoznaczne rozwiązanie. Nie zauważyłem tego bo moje ręczne notatki „patrzą” na wszystko od strony pozostałych czterech kluczowych pól i to rozwiązanie utonęło mi w 3 wariantach dla (b8,b6)=(5,3). I tu wychodzi przewaga komputera nad człowiekiem 😉