Różowe kratki
Jeszcze raz proponuję wpisywanie cyfr w kratki. I jeszcze raz miała być zagadka indukcyjna, ale w porę się pohamowałem, bo byłoby to już jednak przegięcie. Co można bowiem wywnioskować z rozwiązania przykładu? Pewne jest chyba tylko to, że każda mała cyferka na granicy pól oznacza różnicę między liczbami, które powinny się w tych polach znaleźć.
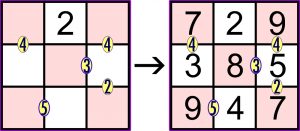
O inne wnioski prowadzące do rekonstrukcji instrukcji znacznie trudniej. A są one następujące:
– w kratkach powinny się znaleźć liczby z zakresu od 1 do 9;
– gdyby wpisać małe cyferki na wszystkich granicach pól, to każda z umieszczonych wokół danego różowego pola byłaby większa od tej, która jest wpisana;
– takie same liczby nie mogą pojawić się w kratkach sąsiadujących w wierszu lub kolumnie.
I to wszystko, a poniższe zadanie czeka na rozwiązanie.
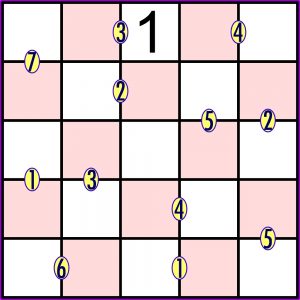
W rozwiązaniu wystarczy podać pięć cyfr na przekątnej – od lewego górnego rogu do prawego dolnego.

Komentarze
Uff, strasznie mylące są te różowe pola.
Po przekątnej: 89134
84195
19741
95193
82739
39214
„gdyby wpisać małe cyferki na wszystkich granicach pól, to każda z umieszczonych wokół danego różowego pola byłaby WIĘKSZA od tej, która jest wpisana;” – z obrazka wynika, że MNIEJSZA.
W sposób równoważny można to wyrazić: Różowe pola są większe od wszystkich białych sąsiadów.
Chodzi o zależność tylko między małymi cyferkami-różnicami wpisywanymi wokół różowego pola. Ujawniona jest tylko najmniejsza z nich.
mp
Mam wątpliwość dotyczącą reguł:
Gdyby tę:
„– gdyby wpisać małe cyferki na wszystkich granicach pól, to każda z umieszczonych wokół danego różowego pola byłaby większa od tej, która jest wpisana;”
… zastosować do przykładowego rozwiązania, to pola 7 i 2 z pierwszego wiersza dają różnicę 5 i teraz nie wiem, co ma być od czego większe?.
A dokładniej nie znajduję takiego odczytania powyższej reguły, która stosuje się bez sprzeczności we wszystkich innych przypadkach.
A może po prostu czas na moją drugą kawę?…
Chodzi o małe cyferki-różnice wpisywane wokół różowego pola. Ujawniona jest tylko najmniejsza z nich.
mp
89134
W takim razie Pole(1,2)=4 a zatem Pole(2,2) może być równe co najwyżej zero – sprzeczność bo musi być co najmniej 1 🙁
Przyjąłem tu założenie, że różowe jest zawsze większe od białego sąsiada, (w przykładzie wszystkie różowe są większe od białych sąsiadów). Ale wynika z tej sprzeczności, że tak nie jest i Pole(2,2) jest równe 8 lub 9 🙂
W przykładzie to nawet każde różowe góruje nad każdym białym.
mp
8 9 1 3 4
Zawsze rozwiązanie zajmuje więcej czasu, jak się nie przeczyta poleceń dokładnie 😉
W polu (4,4) wychodzi mi sprzeczność 🙁
Innym nie wychodzi 🙂
mp
89134
Może źle zrozumieli treść zadania 😉
Mam nadzieję, że początek jest bez zastrzeżeń:
841??
197??
951??
82???
39???
Teraz: P(3,3)+co najmniej 6 =1 + co najmniej 6={7,8,9}=P(3,4)
P(3,4)-co najmniej 6={7,8,9}-co najmniej 6={1,2,3}=P(4,4)
z drugiej strony: P(5,2)-co najmniej 7=9 – co najmniej 7={1,2}=P(5,3)
P(5,3)+1={1,2}+1={2,3}=P(5,4)
P(5,4)+/- co najmniej 2={1,4,5,6,7,8,9}=P(4,4)
A więc P(4,4)={1,4,5,6,7,8,9} przecięcie {1,2,3}={1}
Ale z trzeciej strony mamy:
P(4,2)+co najmniej 5=2+co najmniej 5={7,8,9}=P(4,3)
P(4,3)-4={7,8,9}-4={3,4,5}=P(4,4)
Ponieważ {1} przecięcie z {3,4,5}= zbiór pusty,więc mamy sprzeczność,
bo w P(4,4) nie możemy nic wpisać.
Czy P(a,b) w zapisie oznacza kolumnę a i wiersz b, czy odwrotnie?
mp
Odwrotnie, a-wiersz, b-kolumna. U mnie w przykładzie P(2,3)=7.
Błąd jest przy wyznaczaniu P(5,4)
mp
Niech to gęś…..!!!!!
Widocznie uznałem, że 2 jest zbyt małą liczbą, żeby od niej jeszcze coś odejmować 😉
Zadanie szybko robi się ręcznie.
Ze względu na metodę rozwiązywania nasuwa się dla tego typu łamigłówki nazwa „Fala zwrotna” lub „Powracająca fala”.
Jedyne rozwiązanie:
84195
19741
95193
82739
39214