Efekt falowy
W łamigłówce polidoku, której dotyczył poprzedni wpis, diagram podzielony jest na polimina, czyli wielokąty obejmujące jedną, dwie lub kilka kratek (z reguły nie więcej niż 6) – stąd cząstka „poli-„. Natomiast rozwiązanie stanowi, jak w sudoku, kwadrat łaciński n×n, czyli zawierający w każdym wierszu i kolumnie n różnych cyfr od 1 do n – stąd cząstka „-doku”.
Jeśli obecność kwadratu łacińskiego nie byłaby wymagana, a zamiast niej w instrukcji obsługi znalazłby się jakiś inny warunek, to „-doku” w nazwie straciłoby sens, więc wypadałoby wówczas zastąpić go inną cząstką, związaną oczywiście z nowym warunkiem.
W przypadku poniższego zadania nie mam jednak na razie pomysłu na cząstkę po „poli-„, więc pozostanę przy oryginalnej nazwie japońskiej, która w zapisie transkrypcyjnym brzmi „Hakyū kōka”, czyli „Efekt falowy” lub „Efekt tętnienia”. Skąd takie dziwne określenie? – to zagadka dla wyobraźni po zapoznaniu się z regułami zadania.
Diagram należy wypełnić cyframi tak, aby:
– w każdym poliminie złożonym z x kratek znalazło się x różnych cyfr – od 1 do x;
– między dwiema kratkami z jednakową cyfrą x, znajdującymi się w tym samym wierszu lub kolumnie, było przynajmniej x kratek z innymi cyframi (co najmniej jedna kratka między jedynkami, nie mniej niż dwie między dwójkami itd. – jak w poniższym małym przykładzie).
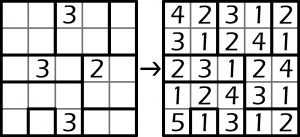
Dziwnemu „Efektowi” stuknie za rok drugi krzyżyk. Zadebiutował na łamach jednego z pism wydawnictwa Nikoli w maju 1998 roku. Powodzenie miał takie sobie, ale w gronie łamigłówek firmowych dotrwał do dziś. Poniżej jeden z „Efektów” należących do twardszych orzechów.

W rozwiązaniu wystarczy podać, które liczby występują nieparzystą liczbę razy na przekątnych diagramu.

Komentarze
Pełne rozwiązanie
1 2 4 3 2 1 5 4 2 3
3 5 1 2 1 4 1 2 1 6
4 1 5 1 3 2 6 1 5 1
1 2 3 4 5 1 2 3 4 2
2 3 1 2 1 3 4 2 1 3
3 1 2 1 4 2 3 1 2 1
6 4 1 3 1 5 2 4 3 2
1 2 3 5 2 4 1 2 1 5
4 1 2 1 3 2 5 1 4 3
5 3 1 2 6 1 4 3 2 1
Życzę jak najszybszego powrotu do zdrowia i wszystkiego najlepszego z okazji Świąt Wielkanocnych.
Czwórka 3 razy, piątka 3 razy
Fantastycznie się rozwiązywało. Powoli, ale bez dłuższego postoju.
1243215423
3512141216
4151326151
1234512342
2312134213
3121423121
6413152432
1235241215
4121325143
5312614321
Na przekątnych nieparzyscie występują 4 i 5.
O ile dobrze liczę to 4 i 5 są po 3 razy.
Zadanie sympatyczne, rozwiązuje się po sznurku, choć czasem trochę postrzępionym.
4 i 5. Łatwe było, szło bez przestojów.
1243215423
3512141216
4151326151
1234512342
2312134213
3121423121
6413152432
1235241215
4121325143
5312614321
Żmudna dłubanina, z oporami do przodu ale ciekawsze od sudoku 😉
Na obu przekątnych razem nieparzystą ilość razy występują 4 (3 razy) i 5 (3 razy). Natomiast oddzielnie na każdej przekątnej: 1 (3 razy) i 2 (3 razy) na jednej przekątnej; a 1 (3 razy), 2 (1 raz), 4 (1 raz) i 5 (1 raz) na drugiej przekątnej.
Na jednej przekątnej: 1554122241, na drugiej: 3112343315
Dla tych, którzy lubią łamigłówki geometryczne, dwie zagadki od pana Naokiego Inaby:
http://pokazywarka.pl/4p770s/ Pozdrawiam 🙂
lewe: 10
prawe: 14
fajne 🙂
Rozwiązanie trochę czasu jednak zajęło (na raty, wieczór i rano) … ale muszę przyznać że dawno nie rozwiązywałem tak fajnej zagadki.
W przyszłości – proszę o więcej tego!
/LG