Dodamino
Domino tradycyjne jest szóstkowe, czyli na kamieniach występują wszystkie kombinacje par cyfr od zera do sześciu, a kamieni jest 28. Częściami tego kompletu są podkomplety złożone z mniejszej liczby kamieni. Na przykład domino trójkowe obejmuje 10 kamieni z kombinacjami par cyfr od zera do trzech (rys. z lewej).
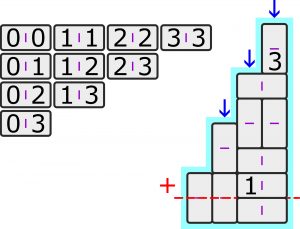
Zadanie polega na ułożeniu z domina trójkowego dodawania o zadanym kształcie i układzie kamieni (rys. z prawej). Każda liczba w dodawaniu (składniki i suma) powinna składać się z różnych cyfr i żadna nie może być ani zaczynać się zerem. Ponadto w kolumnach wskazanych strzałką taka sama cyfra może występować co najwyżej dwa razy. Na dobry początek dwie cyfry ujawniono.

Komentarze
Zadanie da się rozwiązać bez błądzenia:
1. Wszystkie domina złożone z dwóch takich samych cyfr muszą być ułożone pionowo (warunek na liczby z różnych cyfr). [00] nie może być ułożone na początku żadnego składnika, więc zostają dwa pola do rozważenia (druga kolumna na dole i czwarta kolumna w środku). Jeśli wstawimy je do drugiej kolumny, to poznamy jedną cyfrę sumy, ale nie ma możliwości, żeby drugie domino i ewentualna „pożyczka” dała sumę podzielną przez 10. [00] trafia do czwartej kolumny.
2. [11] nie może znaleźć się ani w dolnych dwóch wierszach, ani w trzeciej kolumnie – z obu miejsc wyklucza je postawiona już jedynka. Zostaje górne domino w drugiej kolumnie.
3. Wiersz obok plusa: będą cztery różne cyfry, a 0 nie może być ani w pierwszej, ani w ostatniej (ze względu na [00]), więc będzie w drugiej kolumnie. Podobnie wiersz sumy: odpada pierwsza i ostatnia, a także druga (bo [00] jest już wykorzystane), więc 0 trafi do kolumny trzeciej. Z pozostałych wierszy wykluczamy czwartą kolumnę, pierwsze cyfry oraz wiersze, w których już jest 0. Zostaje tylko jedno pole: trzecia kolumna, trzeci wiersz od dołu.
4. W czwartej kolumnie wszystkie cyfry będą po dwa razy, więc ich suma, to 12. Wyjmujemy jedną cyfrę i sprawdzamy, czy będzie równa sumie pozostałych modulo 10. Spełnione wyłącznie dla 1, które trafia do ostatniego wiersza.
5. W trzeciej kolumnie w wierszu sumy jest 0. W skład sumy wchodzą dwie znane cyfry: 0, 1 oraz 1 z czwartej kolumny. Czyli pozostałe trzy cyfry muszą dać 8. To nam wyklucza pionowe domino dla [22], które trafi do pierwszej kolumny.
6. Uzupełniamy trójkami dwa dolne wiersze.
7. Wolne pole obok 0 uzupełnia 2 (bo pozostałe domina już użyte).
8. [33] nie trafi do czwartej kolumny, bo już są tam dwie trójki, więc będzie w trzeciej.
9. 2 na sam szczyt, co następnie wymusza 1 w ostatnim wolnym polu tej kolumny oraz 2 w ostatnim wolnym polu całej planszy.
___2
___3
__21
__30
_130
_102
2013
2301
Znalazłam 2 rozwiązania:
_ _ _ 1
_ _ _ 3
_ _ 2 3
_ _ 3 0
_ 1 3 0
_ 1 0 2
2 0 1 2
2 3 0 1
_ _ _ 2
_ _ _ 3
_ _ 2 1
_ _ 3 0
_ 1 3 0
_ 1 0 2
2 0 1 3
2 3 0 1
Czy jest więcej?
Pani Olu, jedno rozwiązanie jest błędne. Które i dlaczego?
mp
Nie doczytałam, niestety… Teraz widzę, że liczba 2012 nie spełnia warunków zadania.
2+3+21+30+130+102+2013=2301
___2
___3
__21
__30
_130
_102
2013
——
2301
Przyjemne.
Jest jedno rozwiązanie:
xxx2
xxx3
xx21
xx30
x130
x102
2013
2301
Szybko dochodzimy do wniosku, że trzeba sprawdzić 4 układy 3 kamieni w dwóch pierwszych kolumnach z czego 3 dają sprzeczności.
Nie wiem, jak napisać rozwiązanie, ale spróbuję („x” oznacza puste pole):
x x x 1
x x x 3
x x 2 3
x x 2 0
x 1 2 2
x 1 2 1
3 0 1 0
3 3 0 0
Pionowy kamień (0,2) można odwrócić „do góry nogami”, co utworzy drugie rozwiązanie.
@ Baś
W wierszach nie może być jednakowych cyfr 😉