CDS bis
We wpisie z 7 listopada zamieściłem bardzo trudne, wymagające przy rozwiązywaniu nie lada spostrzegawczości, koncentracji i anielskiej cierpliwości, zadanie CDS (Cyfry Do Strzałek). W komentarzach pojawiły się (ku mojemu zdziwieniu) prośby o CDS z większym diagramem. Obiecałem ich spełnienie, czego niniejszym dotrzymuję, ale obawiam się, że ani nie zaspokoję w pełni czekających na bis, bowiem zadanie wydaje się nieco łatwiejsze, ani nie skłonię do zainteresowania łamigłówką większej liczby osób, ponieważ wciąż jest ona na tyle trudna, że pozostaje elitarną.
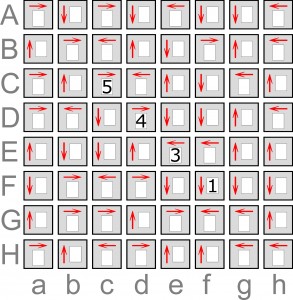
Dysponuję wprawdzie CDS-ami na diagramach 10×10 i 12×12, ale doszedłem do wniosku, że takie giganty nawet w Łamiblogu byłyby przesadą, więc proponuję tylko o jedno oczko więcej, czyli 8×8.
Gwoli przypomnienia objaśnienie:
Do każdej kratki należy wpisać taką cyfrę – z zakresu od 1 do 7 – aby umieszczona obok niej strzałka wskazywała na tyle różnych cyfr, jaka jest wartość wpisanej cyfry. Cztery cyfry są już na swoich miejscach.
I gwoli jasności mały przykład z odpowiednio mniejszym zakresem cyfr:
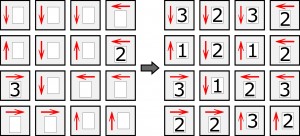
W rozwiązaniu wystarczy podać, ile razy w wypełnionym diagramie występują cyfry, z których żadna nie została na początku ujawniona, czyli 2, 6 i 7.

Komentarze
Na razie zadanie rozwiązał komputer. Znalezienie rozwiązania zajęło mu 22 sekundy, a sprawdzenie, że jest to jedyne rozwiązanie – 70 sekund. Zdaniem komputera zadanie jest nadmiernie ułatwione, poprzez podanie zbędnych informacji. Do tego, by rozwiązanie było dokładnie jedno, wystarczy podanie dwóch cyfr – 5 w Cc i 4 w Dd.
Zadanie rozwiązuje się samo 😉 W algorytmie, który opisałem ostatnio wystarcza jeden cykl, tzn. zawężanie list osobno w każdym z wierszy i kolumn prowadzi prosto do jednoznacznego rozwiązania.
Nieco bardziej serio: jest jeden przestój mniej więcej przy połowie zapełnionej planszy, wtedy chyba najwygodniej byłoby strzelać.
Nie ma na planszy żadnej siódemki i może to jest kluczem do mniejszego skomplikowania zadania, niż poprzednio.
43453564
13214214
61532461
51244325
42143433
12222122
43251555
43224544
2×15
6×3
7×0
15 dwójek i 3 szóstki; siódemek nie ma.
Zadanie, choć większe niż poprzednio, okazało się dużo łatwiejsze. Ani razu nie trzeba było robić dłuższych analiz, bo kolejne cyfry same wychodziły. O ile w tamtym zadaniu trzeba było mozolnie ograniczać zakresy liczb w poszczególnych kratkach, to w tym kilka razy dało się od razu skorzystać z tego, że w danej części wiersza czy kolumny musi być n różnych liczb i od razu je wpisać. Dużym ułatwieniem był też układ strzałek w wierszu F, z którego wynikało, że mogą być tam tylko jedynki i dwójki.
Dwójek w rozwiązaniu jest 15, szóstek – 3, a siódemki ani jednej.
Komputer sprawdził, że po usunięciu wszystkich ujawnionych liczb, zadanie ma 899 rozwiązań. Do tego, by otrzymać właściwe, wystarczy ujawnienie dwóch cyfr, np. 5 w Cc i 4 w Dd albo 5 w Cc i 3 w Ee. Można otrzymać jednoznaczne rozwiązanie (oczywiście inne), ujawniając tylko jedną liczbę – 7 w Ha lub w Hh. Jest to zresztą jedyne przy tym układzie strzałek rozwiązanie, w którym występują siódemki.
Liczby 2,6,7 padają odpowiednio 15,3,0 razy.
Poniżej rozwiązanie:
4 3 4 5 3 5 6 4
1 3 2 1 4 2 1 4
6 1 5 3 2 4 6 1
5 1 2 4 4 3 2 5
4 2 1 4 3 4 3 3
1 2 2 2 2 1 2 2
4 3 2 5 1 5 5 5
4 3 2 2 4 5 4 4
To zadnie w porównaniu do poprzedniego było dużo prostsze. Po przekroczeniu pewnego momentu właściwie samo się rozwiązało.
43453564
13214214
61532461
51244325
42143433
12222122
43251555
43224544
Jedyne rozwiązanie:
4,3,4,5,3,5,6,4
1,3,2,1,4,2,1,4
6,1,5,3,2,4,6,1
5,1,2,4,4,3,2,5
4,2,1,4,3,4,3,3
1,2,2,2,2,1,2,2
4,3,2,5,1,5,5,5
4,3,2,2,4,5,4,4
Zadanie okazało się łatwiejsze od poprzedniego.
Co prawda średnia, początkowa długość list była większa
ale za to końcowe listy miały co najwyżej dwa elementy
dając automatycznie rozwiązanie.
Poprzednim razem końcowe listy nie dawały rozwiązania i
potrzebny był ostatni etap poszukiwań.
Podtrzymuję hipotezę, że w tym zadaniu o trudności nie
decyduje rozmiar kwadratu lecz układ strzałek.
Moim zdaniem korzystny układ strzałek to taki w którym
na danym kierunku występuje jak najwięcej strzałek
zwróconych przeciwnie, najlepiej grotami do siebie.
Oraz kiedy strzałki blisko brzegu zwrócone są na zewnątrz.
Te dwa warunki do pewnego stopnia się wykluczają ale
godzi je układ strzałek w dwóch blokach -><-.
W poprzednim zadaniu takich układów w ogóle nie było na
kierunku poziomym a w ostatnim były na obu kierunkach.
Weryfikacja tej hipotezy (trudność zadania zależy głównie od układu strzałek a nie od rozmiaru kwadratu) była by możliwa przez rozwiązanie, sygnalizowanego przez Gospodarza, zadania 12 x 12, ale nic nie sugeruję……. 🙂 no, może gdzieś za rok, na przerwę świąteczno-noworoczną ?