Odrzutek
Wybierane do dziesiątego „Omnibusa” zadania przechodzą dość ostrą selekcję. Konsultanci odrzucają przede wszystkim to, co uważają za zbyt trudne, a zwłaszcza zniechęcające perspektywą żmudnej dłubaniny. Taki los spotkał więc poniższe zadanie. Czy słusznie?
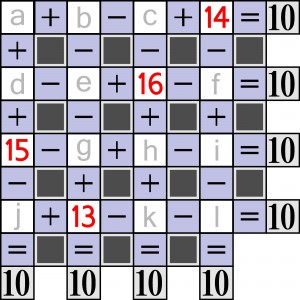
Patrząc na diagram łatwo się domyślić, o co chodzi: w białych kratkach powinny pojawić się liczby od 1 do 16 rozmieszczone tak, aby w wierszach i kolumnach powstały poprawne równości, których „okolicznościowe” wyniki są podane. Ponadto liczby od 13 do 16 znajdują się już na swoich miejscach, więc wystarczy zamiast szarych liter wpisać pozostałe – od 1 do 12.
Czy droga do celu „na piechotę” rzeczywiście wiedzie przez wyboiste układy równań, czy może uda się znaleźć jakiś w miarę łagodny skrót?

Komentarze
Panie Marku. Poprzedni wpis dobrze pokazuje, że w Łamiblogu w komentarzach powinna być stosowana czcionka o stałej szerokości znaków. Polecam Czcionkę „Courier New”. Czy można poprosić administratora blogu, aby zastosował taką czcionkę dla tego blogu? To by znacznie ułatwiło życie wszystkim komentatorom.
Ps. W razie czego służę pomocą administratorowi, aby wyjaśnić istotę problemu!
Przekażę prośbę administratorowi.
mp
kolejno rzędami:
1 5 10 14
3 2 16 7
15 6 12 11
9 13 4 8
Rozwiązanie znalezione przez dłubaninę (czyli bez łagodnego skrótu):
a=1
b=5
c=10
d=3
e=2
f=7
g=6
h=12
i=11
j=9
k=4
l=8
a=1, b=5, c=10, d=3, e=2, f=7, g=6, h=12, i=11, j=9, k=4, l=8.
http://pokazywarka.pl/6sgmlz/
{A,B,C,D,E,F,G,H,I,J,K,L}={1,5,10,3,2,7,6,12,11,9,4,8}
Z układu 8 równań sprytnie otrzymujemy A+E+F+G=16. Znajdujemy (bez kompa) 9 czteroelementowych podzbiorów zbioru {1,2,…,10} dających sumę = 16. Mając A, E, F, G możemy obliczyć B, C, D, J. (Zmienne H, I, K, L tworzą odrębną podprzestrzeń). Dla każdego takiego 4-elementowego podzbioru sprawdzamy 4!=24 permutacji patrząc czy zmienne A, B, C, D, E, F, G, J są różnymi liczbami ze zbioru {1, 2,…,12}. Ten ostatni krok na piechotę jest dość żmudny ale prosty programik albo Excel załatwia sprawę. Otrzymujemy 3 możliwe podzbiory A, B, C, D, E, F, G, J. Teraz sprawdzamy pozostałe zmienne H, I, K, L. Okazuje się, że tylko w jednym przypadku da się uzupełnić układ.
a=1, b=5, c=10
d=3, e=2, f=7
g=6, h=12, i=11
j=9, k=4 ,l=8
a=1 b=5 c=10 d=3 e=2 f=7 g=6 h=12 i=11 j=9 k=4 l=8
Z kartką i ołówkiem zajęło mi 1,5 h. ale to tylko dlatego, że pod „a” zacząłem podkładać od największej możliwej (czyli 5, bo resztę mi się udało wykluczyć) w dół. Dodatkowy warunek jaki mi wyszedł to a+d <= 7 oraz a+b <=8.
Eureka ! Można znacznie przyśpieszyć. Ze znalezionego związku A+E+F+G=16 i z drugiego równania poziomego wynika, że A+D+G=10. Tylko 4 układy spełniają to równanie. Razy 3!=6 to daje tylko 24 kombinacje do sprawdzenia. Każda z tych kombinacji sama się uzupełnia (do rozwiązania albo sprzeczności). 🙂
Eureka bis! Z A+E+F+G=16 i z drugiego równania pionowego mamy A+B+F=13. Podstawiamy do pierwszego równania poziomego A+B=13-F i mamy F+C=17 a to daje już tylko 4*2!=8 kombinacji do sprawdzenia. :))