Chęć na rtęć
Przed 300 laty Fahrenheit wynalazł termometr rtęciowy, którego żywot właśnie dobiega końca. Przetrwa zapewne tylko w łamigłówkowej rzeczywistości wirtualnej, do której na początku XXI wieku przenieśli go Holendrzy. W takiej formie toksyczne właściwości rtęci są niegroźne, a fizyczne – związane z rozszerzalnością cieplną – pożądane.
„Termometry” należą do zadań logicznych wysokiej próby. Zwykle rozwiązywanie polega na przemian na oznaczaniu pól, do których rtęć musi dotrzeć oraz przekreślaniu tych, w których na pewno się nie pojawi. Nie brak jednak momentów, gdy ten dość prosty schemat komplikuje się – jak w poniższym zadaniu, pochodzącym z łamigłówkowych mistrzostw Chorwacji.
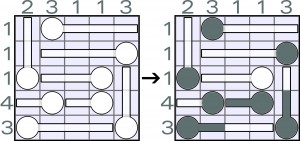
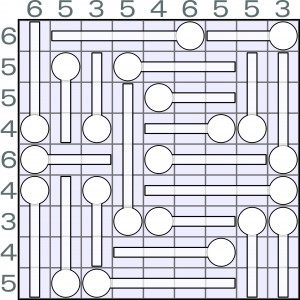
Do termometrów należy „nalać” rtęci (nie koniecznie do wszystkich i w różnym stopniu) – tak, aby każdy z rtęcią wskazywał odpowiednią temperaturę określoną pośrednio przez liczby obok diagramu. Liczby te oznaczają, w ilu kratkach w danym wierszu lub kolumnie powinna pojawić się rtęć. Termometry są sprawne, więc rtęć nigdzie nie może się przerwać, czyli jeśli „naciągnie” np. na trzecią kratkę, to musi być obecna także w dwóch poprzednich oraz oczywiście w kratce ze zbiorniczkiem (kółko).
Jako rozwiązanie wystarczy podać, w ilu termometrach rtęć jest tylko w dwóch kratkach (zbiorniczek i następna kratka).

Komentarze
http://pokazywarka.pl/cgadu9/
Rtęć w dwóch kratkach jest w siedmiu termometrach.
W siedmiu termometrach rtęć jest w dwóch kratkach.
http://i.imgur.com/tiMEsev.jpg
Rtęć w dwóch kratkach występuje w siedmiu termometrach.
Fajne 🙂
W jakimś notatniku powinno wyglądać lepiej:
_====O__O
_O_O===__
_║__O==║_
O____=OO_
O=__O==_O
O_O║____O
║__O___O_
║____=O║_
║OO=___║_
Termometrów nie długich, nie krótkich, lecz w sam raz, jest siedem.
7
Zadanie ciekawe dla obu metod rozwiązywania: zarówno umysłowo jak i komputerowo.
Po tym moim dyskusyjnym powyższym rozgraniczeniu dodam, że większą satysfakcję dało mi napisanie programu.
Na piechotę jest interesująco, ale w pewnym miejscu musiałbym użyć technik, które są dla mnie małorozrywkowe, więc udałem się w mroczne czeluście algorytmów.
Próba „zhakowania” zadania:
W warunkach zadania mamy:
– 22 termometry o znanych pojemnościach
– 42 krople rtęci, które należy umieścić w tych termometrach
Rozmieściłem te 42 krople w sposób losowy, a następnie policzyłem ilość termometrów z zawartością dwóch kropel.
Procedurę powtórzyłem wielokrotnie.
Średni wynik to 6 z hakiem.
Po zaokrągleniu wyniku do liczby całkowitej otrzymałem 6.
Hak okazał się za mały 😉
apartado,
Głowa do góry! To zadanie można rozwiązać na piechotę i to nawet bez ołówka i gumki! Podpowiedź: w 5. i 6. kolumnie są wyłącznie poziome – i to te same – termometry.
Jeden z ostatnich komentarzy @Spytko z Melsztyna spowodował,
że ponownie pochyliłem się nad tym zadaniem.
Jak wiemy oryginalne zadanie ma jedno rozwiązanie.
Wyobraźmy sobie, że powielając zadanie oryginalne
(o rozmiarach 9×9 i 22 termometrach) tworzymy czterokrotnie
większe zadanie o rozmiarach 18×18 i o ilości termometrów równej 88 (dodatkowo podwajamy liczby obok diagramu – dla poszczególnych wierszy oraz kolumn).
Pytanie:
czy takie zadanie też będzie miało jedno rozwiązanie?
Nikt nie odpowiedział na postawione przeze mnie pytanie.
Postanowiłem nie czekać dłużej.
Skonstruowane w ten sposób zadanie, ma więcej niż jedno rozwiązanie.