Duo parcelek
Typowy relaksowy diagram KenKen podzielony jest na wiele działek. Rzadkością są działki obejmujące więcej niż 5 kratek, więc w przypadku diagramu 5×5 jest ich zazwyczaj 7-8, a w diagramie 6×6 już nawet kilkanaście. Nie wiem, kto pierwszy postawił pytanie o minimalną liczbę działek dla diagramu n×n, przy której łamigłówka ma jedno rozwiązanie, ale szukanie odpowiedzi doprowadziło do ciekawych rezultatów. Poniżej jeden z nich.
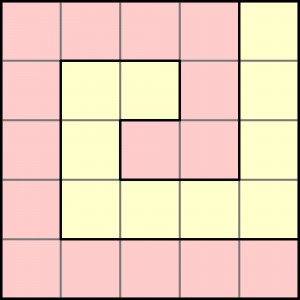
Diagram 5×5 rozparcelowany jest tylko na dwie działki. Wyniki działań na cyfrach, które powinny się znaleźć w każdej, są następujące: działka różowa – 43200, działka żółta – 39. Rodzaju działań łatwo się domyślić. W każdym rzędzie i w każdej kolumnie – jak to w KenKenie – powinno pojawić się pięć różnych cyfr – od 1 do 5.
Czy rozwiązanie jest jedno? A jeżeli tak, to jakie? A jeżeli nie, to co zmienić (zmiana powinna być jak najmniejsza i wyłącznie liczbowa), aby było tylko jedno.

Komentarze
Rozwiązanie jest jedno.
W działce różowej iloczyn liczb wynosi 43200. Rozkładając tą liczbę na czynniki pierwsze otrzymujemy: 43200 = 2^6 * 3^3 * 5^2
To oznacza, że w różowej działce znajdują się dwie piątki oraz trzy trójki. Zatem w żółtej działce mamy dwie trójki oraz trzy piątki – one sumują się do 21, czyli pozostałe 5 liczb musi dawać sumę 18, przy czym nie może to już być żadna piątka ani trójka. Jedyna możliwość, to cztery czwórki i jedna dwójka.
W pierwszej kolejności wpisujemy cztery czwórki do działki żółtej – jest tylko jedna możliwość. Następnie do żółtej wpisujemy trzy piątki – znowu jedna możliwość. W kolejnym ruchu wpisujemy do żółtej dwie trójki – znowu jedna możliwość i dwójkę – w ostatnie wolne pole działki żółtej.
Reszta leci jak po sznurku: najpierw brakująca czwórka, potem brakujące dwie piątki, reszta jest banalna…
51234
25413
34125
13542
42351
Wg mnie rozwiązanie jest jedno
5 1 2 3 4
2 5 4 1 3
3 4 1 2 5
1 3 5 4 2
4 2 3 5 1
Dosyć szybko znalazłem rozwiązanie.
1. Znalazłem pierwszy lepszy zestaw cyfr składający się na sumę 39, który da się wstawić tak, by cyfry nie powtarzały się w wierszach/kolumnach.
2. Sprawdziłem iloczyn pozostałych cyfr, okazało się, że jest zbyt mały. Dokładnie 0,8 pożądanego. A to znaczyło, że muszę w żółtym bloku podmienić jedną piątkę na czwórkę.
3. Cyfry w bloku żółtym ułożyć dało się już tylko w jeden sposób, a później wypełnienie reszty było formalnością.
51234
25413
34125
13542
42351
Tak na szybko nie widzę innego zestawu cyfr dla żółtego bloku, więc wydaje się, że to jest jedyne rozwiązanie.
Rozwiązanie jest tylko jedno.
Poniżej krok po kroku jak do niego doszedłem. Kolumny oznaczam literkami od A do E, wiersze cyframi 1-5.
1. mnożenie składające się z dokładnie 15 cyfr musi wyglądać następująco: 5*5*4*3*3*3*2*2*2*2*1*1*1*1*1
2. zatem na pozycji E5 musi stać ‚1’
3. ‚4’ pojawi się tylko raz więc będzie na pozycji A5
4. jedna z ‚5’ pojawi się w wierszu 5, druga w kolumnie A, ale z uwagi na to, że więcej ‚5’ już nie będzie musi to być pole A1
5. analogicznie ‚3’: dwie będą w wierszu 5 oraz kolumnie A, trzecia z nich musi być na polu D1
6. ‚2’ natomiast musi pojawić się na polu D3
7. można teraz postawić dwie ‚1’ na C3 oraz D2, następnie na B1 i A4
8. następnie stawiamy ‚2’ na C1, A2, B5
9. wreszcie ‚3’ stawiamy na A3 oraz C5 a następnie ‚5’ na D4
10. dalej leci już po sznureczku: brakującymi cyframi uzupełniamy wiersz 1 – ‚4’, oraz kolumnę D – ‚4’, w wierszu 3 wpisujemy ‚4’ oraz ‚5’, w kolumnie E brakujące ‚3’ oraz ‚2’, w wierszu 2 ‚5’ oraz ‚4’ no i w wierszu 4 ‚3’ i ‚5’
voilà – jak widać do rozwiązania dochodzimy w sposób jednoznaczny
obrazkowo: http://bankfotek.pl/view/1935903
poprawka 😉 http://bankfotek.pl/view/1935904
Zdaje się, że jedno: na działce żółtej od środka kolejno 4543542534, na różowej 121321523142351.
Oczywiście bzdury napisałem w moim wyjaśnieniu, bo sama wymiana piątki na czwórkę zmieniłaby sumę na mniejszą. A teraz sam już nie pamiętam, co zrobiłem między punktami 1 i 2. Czyżbym znalazł jednak sumę 40? No to mam następną zagadkę 😉
Skruszony zaproponuję inne wyjaśnienie:
43200 = 5^2 * 3^3 * 4^x * 2^y
Czyli na sumę będą składały się:
5*3 + 3*2 + 4*(5-x) + 2*(5-y) (jedynki są tutaj nierealne, można sprawdzić)
4*(5-x) + 2*(5-y) = 18
x+y = 5
Czyli: x = 4, y = 1
51234
25413
34125
13542
42351
51234
25413
34125
13542
42351
Jest tylko jedno rozwiązanie:
51234
25413
34125
13542
42351
Zadanie perełka ale łatwe. Idzie jak po sznurku bez rozwidleń.
Liczbę 43200 rozkładamy na czynniki.
Cyfry przyporządkowujemy do „węży” w kolejności: 5-ki,3-ki,4…,2…,1….
Cyfry ustawiamy w „wężach” w następującej kolejności: 4-ki,1-ki,2…,5…,3….
5 1 2 3 4
2 5 4 1 3
3 4 1 2 5
1 3 5 4 2
4 2 3 5 1
jednoznaczne
Rozwiązanie jest jedno:
51234
25413
34125
13542
42351
Można teraz zapytać. Skoro dla liczb (39, 43200) rozwiązanie jest jedno, to czy istnieją jeszcze takie pary liczb (x, y) dla których też otrzymujemy jedno rozwiązanie? (1)
A teraz z innej KenKenowej beczki.
W październikowym „Umyśle giętkim” w odpowiedziach do zadań z numeru sierpniowego mamy odpowiedź na pierwsze zadanie: „można pozostawić tylko pięć liczb, a rozwiązanie nadal będzie tylko jedno”. W pewnym sensie odpowiedź jest poprawna. Ale czy pozostawione liczby tworzą zbiór krytyczny? (2)
PS Dlaczego na internetowej stronie „Świata Nauki” zniknął wrześniowy „Umysł giętki”? (3)
Odpowiadam:
(1) Znam jedną inną parę, dla której też jest jedno rozwiązanie (oczywiście przy identycznych działkach). Nie wykluczam, że znajdą się jeszcze jakieś.
(2) Chyba nie, tzn. wiem, że przy czterech pozostawionych liczbach też jest jedno rozwiązanie, ale nie mogę znaleźć teraz rozwiązania z tą czwórką, więc nie wiem, czy jest ona podzbiorem zamieszczonej piątki.
(3) Bardzo rzadko zaglądam na stronę internetową „ŚN”. Informacja o zniknięciu jest dla mnie niespodzianką. Podejrzewam, że zmieniła się koncepcja, tzn. zamieszczany będzie tylko początek „Umysłu”, ale dlaczego w takim razie zniknął całkowicie? – oto zagadka.
Zdravi
mp
(2) Spośród pozostawionych pięciu liczb można usunąć górną jedenastkę i nadal będzie tylko jedno rozwiązanie.
Spóźnionym rzutem na taśmę: rzędami od góry 51234, 25413, 34125, 13542, 42351. Etapy rozumowania: w żółtej części w kolumnie i rzędzie tam gdzie po 4 cyfry muszą być 5, 4 i 3 po 2 razy i raz 2 na przecięciu, więc suma ostatnich 3 cyfr musi być 13, czyli 5, 4 i 4; jak się sprawdzi iloczyn tego co zostało, to jest ile trzeba. Potem ładnie dają się wpisać wszystkie jedynki, rzeczone 5, 4 i 4, i właściwie wszystko.