Macki dla Królików
Mam na tapecie kolejny Omnibus – trzeci zimowy, a dziewiąty w ogóle. Będzie w nim między innymi trochę całkiem nowych rodzajów zadań logicznych. Pomyślałem, że można by w związku z tym potraktować Łamiblog jak poligon doświadczalny dla „przetarcia” tych zadań, a Szanownych Czytelników jak… króliki doświadczalne
A zatem, Drogie Króliczki, oto nowy, nieco zakręcony rodzaj łamigłówki zwanej mackami. Starałem się sformułować reguły jak najzwięźlej, ale nie mam pewności, czy nie straciła na tym komunikatywność. Więc niniejszym się upewniam.
Liczby wysuwają macki poziomo i pionowo w czterech kierunkach. Każda sięga mackami w sumie tylu pustych kółek, jaka jest jej wartość. Wszystkie macki stykają się, ale tylko po dwie, tylko końcami i wyłącznie pod kątem prostym; zatem żaden koniec nie pozostaje wolny – styka się z końcem innej, jednej i tylko jednej macki.
Macki nie muszą dotrzeć do wszystkich pustych kółek i żadna nie sięga kółka z liczbą.
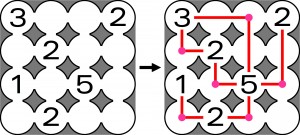
Przykład:
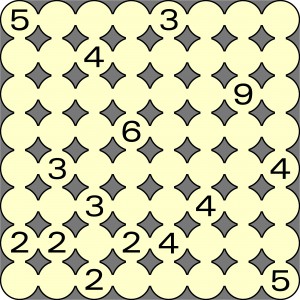
Zadanie polega oczywiście na narysowaniu wszystkich macek.
Jako rozwiązanie wystarczy podać liczbę pól niemacanych (w przykładzie jest jedno).

Komentarze
http://pokazywarka.pl/macki-2/
8 niemacanych pól.
8
Jest 8 pustych pól
6 niemacanych – taki strzał bez rozwiązywania ?
Założenie:
Wszystkich pól jest M*M (8*8= 64)
Liczby sumują się do N (58)
Pól z podwójnymi mackami jest tyle co liczb.
Bez macek zostaje M*M-N = 64 – 58 = 6
Pozdrawiam (i próbuje rozwiązać) 🙂
I już wiem, że mój strzał był niecelny…
Niemacanych pól zostaje 8
Rozwiązanie tu:
https://app.box.com/s/i15ojghbeoewn9au5xol8jumr5i6nd3p
Pozdrawiam
ciekawa odmiana ,,wypustek”:)
8 pól niemacanych
rząd I pola 4 i 8 od lewej
rząd II pola 2,6 i 8 od lewej
rząd III pole 2 od lewej
rząd V pole 5 od lewej
rząd VIII pole 1 od lewej
reszta macane (17 załamań)
Jest 8 pól niemacanych.
Liczba pól niemacanych nie stanowi po prostu wyniku odejmowania sumy wartości liczbowych od łącznej liczby pól w diagramie, lecz wyraża się następującym wzorem:
liczba pól niemacanych = łączna liczba pól – (liczba pól zawierających wartość liczbową + suma wszystkich wartości liczbowych – liczba uścisków macek)
A ponieważ liczba macek wysuwających się z liczbowego pola nie jest ściśle określona, pierwsza i ostatnia spośród trzech wartości umieszczonych powyżej w nawiasie nie są tożsame i nie muszą się znieść (aczkolwiek mogą, co ma miejsce w przykładzie).
Rozwiązanie, do którego można dojść „po sznurku”, poczynając od lewej górnej piątki, przedstawia się według sformułowanego wzoru następująco:
8 = 64 – (15 + 58 – 17)
A tak wygląda obrazek:
http://pokazywarka.pl/srcmta/
8 pól niemacanych
http://bankfotek.pl/view/1938331
8 nie macanych