Podstępne 3 po 3
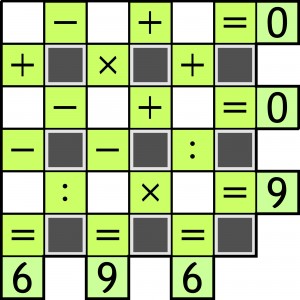
Ten rodzaj zadań należy już właściwie do klasyki. Wytrawni główkołamacze orientują się więc bez instrukcji, że do białych kratek należy wpisać dziewięć różnych cyfr – od 1 do 9 – tak, aby w trzech wierszach i trzech kolumnach powstały poprawne równości, których wyniki są podane.
Wypada jeszcze dodać (choć dotyczy to tylko jednej kolumny), że działania w każdym rzędzie należy wykonywać kolejno – od lewej do prawej i od góry do dołu, czyli bez uwzględniania pierwszeństwa mnożenia i dzielenia.
Zadanie jest jednak nieco podstępne, a triku trzeba się domyślić w trakcie rozwiązywania. Podpowiem tylko, że bez wydrukowania lub przerysowania diagramu rozwiązywanie jest bardzo trudne.

Komentarze
Na pierwszy rzut oka, dolny wiersz jest ciekawy.
Dolny wiersz bez uwzględnienia kolejności działań daje tylko jedną możliwość, która upada wraz z próbą wypełnienia prawej kolumny
No wie Pan… Jak można było nas tak wkręcić. Zakręcić 🙂
http://pokazywarka.pl/d6nnec/
Trzeba kartkę z diagramem odwrócić „do góry nogami”.
4×9/6=6
2+3-5=0
7+1-8=0
Dobór cyfr w wynikach umożliwia obrót planszy o 180 stopni. Po tym zabiegu znalazłem rozwiązanie:
4 9 6
2 3 5
7 1 8
Podobny trik wykorzystany jest w filmiku „łamigłówkowym”:
https://www.youtube.com/watch?v=quFDJo3K0ac
Wydaje mi się, że to wszystko jest do góry nogami 😉
A oto i wynik http://i.imgur.com/XvigHOa.png
W dolnym rzędzie musi być 6/2*3=9 co powoduje, iż drugiej i trzeciej kolumny nie da się ułożyć. Zdaje się, że diagram trzeba wydrukować i obrócić o 180 stopni.
Po odwróceniu diagramu o 180st kolejne liczby to (rzędami): 496 235 718
Zadanie ma rozwiązanie dopiero po obróceniu planszy do góry nogami. Oto jedyne rozwiązanie: 496235718.
Niestety nie udało mi się znaleźć rozwiązania zadania „wprost”, nawet mogę udowodnić, że takiego nie ma. Jeżeli jednak odwrócimy diagram to powstaje zadanie z następującym rozwiązaniem:
4 9 6
2 3 5
7 1 8
Diagram jest odwrócony.Poziomo:
6=4×9:6
0=2+3-5
0=7+1-8
Chmmm…. Siedzę nad tym zadaniem od kilku dni i jestem prawie pewien, że nie ma ono rozwiązania.
Spójrzmy na dolny rząd. Umieśćmy w nim liczby a, b i c.
Wtedy (a/b)*c = 9. Albo inaczej: a*c / b = 9
Gdyby któraś z liczb a lub c była dziewiątką, np. a, to wtedy b = c – sprzeczność.
Gdyby b=9, bo wtedy a*c = 81 – niemożliwe.
Zatem żadna z liczb a, b, c nie jest dziewiątką.
To znaczy, że iloczyn a*c musi być podzielny przez 9 – to jest możliwe tylko wtedy, gdy a=3, c=6, lub na odwrót. A wtedy b=2.
Teraz spójrzmy na środkową kolumnę… Niech dwie górne liczby w tej kolumnie będą równe d i e. Mamy d * e – b = 9. Czyli d * e = 11.
A to jest niemożliwe, bowiem 11 to liczba pierwsza, a taka nie może pojawić się w diagramie.
Mam wrażenie, że gdzieś robię błąd 😉
Proszę pamiętać o podstępie (dość zresztą „perfidnym” 🙂 )
mp
Podpowiedź sugeruje, że warto tabelkę obrócić o 180 stopni.
Ale po obrocie nie mogę znaleźć rozwiązania.
Za to rozwiązałem zadanie podobne:
https://drive.google.com/file/d/0Bwo1QFzne66raXpsN0RENkJMVWM/view?usp=sharing
No tak… Nie wydrukowałem, nie przerysowałem 🙂