Przedsmak
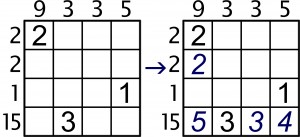
Zmagam się z kolejnym, już ósmym Omnibusem, który – jeśli wszystko dobrze pójdzie – ukaże się w połowie czerwca. Postanowiłem dla zachęty przedstawić Państwu jedno z fajniejszych (moim zdaniem) zadań logicznych, jakie się w nim znajdą. Jego fajność wiąże się z pewną regułą, której nie ujawnię. Inaczej mówiąc, proponuję Państwu zagadkę indukcyjną, czyli rozszyfrowanie zasad zabawy w oparciu o mały przykład z rozwiązaniem, który wygląda tak:
W oczy się rzuca, że w niektóre kratki należy wpisać cyfry – takie, aby suma wszystkich liczb w danym wierszu (kolumnie) była równa liczbie podanej przed lub nad rzędem. Ale to nie wszystko. Jest jeszcze jeden mały waruneczek, który stanowi orzeszek do rozgryzienia. Jaki?
A kto sobie z tym poradzi, ten bez trudu rozwiąże poniższe zadanie.
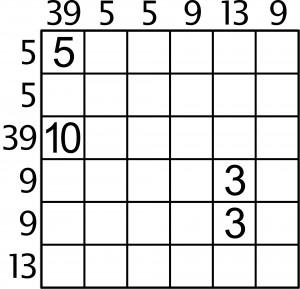

Komentarze
Jeśli są dwie takie same cyfry/liczby w rzędzie lub kolumnie, to stoją obok siebie:
5 _ _ _ _ _
_ _ _ _ 2 3
10 5 5 9 4 6
6 _ _ _ 3 _
6 _ _ _ 3 _
12 _ _ _ 1 _
5 _ _ _ _ _
3 _ _ 2 _ _
10 5 1 7 7 9
4 _ 2 _ 3 _
4 _ 2 _ 3 _
13 _ _ _ _ _
Warunek powinien być taki, aby rozwiązanie zadania – podobnie jak przykładu – było jedno.
mp
może warunek dodatkowy mówiący o tym, że obszar niewypełniony liczbami musi być spójny?
Obszar z daną liczbą musi być tylko jeden, czyli kratki z wpisaną taką samą liczbą muszą tworzyć spójny obszar.
Nie jestem jeszcze pewien czy muszą być to obszary z kolejnymi liczbami…
I nie wiem jeszcze czy obszary mogą mieć dowolne kształty…
Ale skoro mowa o jednym, małym waruneczku, to moim zdaniem brzmi on:
kratki z tą sama liczbą muszą tworzyć jeden, spójny obszar.
Teraz zabieram się za poszukiwanie rozwiązania…
> Warunek powinien być taki, aby rozwiązanie zadania – podobnie jak
> przykładu – było jedno.
Wiem 🙂 Wysłałam tę propozycję, żeby wybadać teren. Gdyby nie ujawnił Pan tego komentarza, mogłoby to oznaczać, że jestem za blisko.
To może warunek, mówiący, że do kwadratu o boku równym n kratek, należy wpisać co najmniej jeden raz każdą z liczb od 1 do n+1 i w dodatku nie można wpisać liczb większych od n+1 ?
Zbyt zakręcone
mp
Każda umieszczona w diagramie liczba musi być równa łącznej liczbie kratek w danym wierszu i danej kolumnie, w których również znajdują się liczby.
Rozwiązanie diagramu 6×6:
5 _ _ _ _ _
5 _ _ _ _ _
10 5 5 6 7 6
6 _ _ _ 3 _
6 _ _ _ 3 _
7 _ _ 3 _ 3
Brawo! Jest Pan pierwszym „odkrywcą”.
mp
PS warunek nie jest zbyt precyzyjnie sformułowany, ale łatwo się domyślić, o co chodzi.
Moje rozumowanie jest takie, że jeśli jest dodatkowy warunek, to w sytuacji gdy są dwie bądź więcej możliwości uzyskania zadanych sum, musi to być coś takiego, co te wszystkie inne możliwości wykluczy. W tym przypadku widzę tylko dwa rozwiązania, mianowicie dwójkę z drugiego rzędu rozbjamy na dwie jedynki w kolumnach – od lewej – pierwszej i trzeciej, wtedy w dolnym rzędzie pojawia się w tych kolumnach 6 (zamiast 5) i 2 (zamiast 3). Co dawałoby od góry patrząc 2, 0, 0, 0; 1, 0, 1, 0; 0, 0, 0, 1; 6, 3, 2, 4. Jest jeszcze jedna możliwość: 2, 0, 0, 0; 1, 0, 0, 1; 0, 0, 0, 1; 6, 3, 3, 3. Najprostszy warunek to w tej sytuacji taki, że musi być uwzględniona co najmniej raz każda liczba pomiędzy najmniejszą a największą, czyli w przykładzie od 1 do 5, a w alternatywnych nie jest to spełnione, bo brakuje albo 5, albo i 4, i 5. Cdn.
Tym tropem szło kilka osób, ale czy wówczas rozwiązanie zadania (nie przykładu) jest tylko jedno?
mp
PS jak dotąd (poniedziałek, samo południe) właściwy warunek znalazła jedna osoba.
A może warunek mówiący, że największa liczba w każdym spójnym obszarze określa ilość pól wchodzący w skład tego obszaru ?
Bez dodatkowego warunku udało mi się znaleźć sześć rozwiązań przykładu i na 99% jestem pewien, że innych nie ma. Ostatnie (właściwe) rozwiązanie różni się tym, że cyfry, które zostały wpisane do kwadratu są kolejnymi cyframi naturalnymi (nie uwzględniając powtórzeń). Więc może to jest ten dodatkowy warunek?
http://bankfotek.pl/view/1888128
Nie.
mp
zaczyna mi brakować pomysłów…
a może warunek mówiący o tym, że żadna z cyfr nie występuje jednocześnie w więcej niż jednej kolumnie i w więcej niż jednym wierszu?
Nie bardzo rozumiem – przecież w przykładzie dwójka występuje w dwóch wierszach, a trójka w dwóch kolumnach.
mp
Może precyzyjniej byłoby tak:
Zawartość każdego niepustego pola kompletnego diagramu stanowi łączną liczbę pozostałych niepustych pól w danym rzędzie i danej kolumnie.
Albo tak:
Jeżeli dane pole nie jest puste, to jego zawartość informuje o tym, jak wiele spośród pól z tego samego rzędu lub tej samej kolumny również zawiera (spełniającą ten warunek) liczbę.
U mnie jest tak:
W wierszu i kolumnie, na przecięciu których znajduje się liczba X, musi być w sumie tyle innych liczb, jaka jest wartość X.
Może być?
mp
Jeśli w dwóch rzędach bądź kolumnach suma jest taka sama, to składniki są identyczne i w tej samej kolejności, czyli 2=2+0+0+0; 3=0+0+0+3. Ta sama kolejność musi być, bo inaczej dobre byłoby też rozwiązanie pierwsze od lewej z tych co zaprezentował @stud (dzięki za ten rysunek, bardzo pomaga).
Wtedy w zadaniu właściwym dostajemy rzędami od góry: 5, 0, 0, 0, 0, 0; 5, 0, 0, 0, 0, 0; 10, 5, 5, 6, 7, 6; 6, 0, 0, 0, 3, 0; 6, 0, 0, 0, 3, 0; 7, 0, 0, 3, 0, 3. Okazuje się, że jeśli suma jest np. 39, to rozkład na składniki jest taki sam, niezależnie czy mamy wiersz, czy kolumnę, ale tego bezpośrednio z pierwszego rysunku wywieść się nie da.
Rozwiązanie jest poprawne i opisany warunek istotnie w tym przypadku „działa”, ale to nie jest TEN warunek. Do „Omnibusa” dałem zadania, w rozwiązaniach których przy tej samej sumie rozkłady na składniki nie są identyczne.
mp
O! Zdziwiłem się, że mój warunek jest zły…
Dzisiaj będę miał czas przysiąść do tego zadania… a nóż sie uda 🙂
Chodziło mi o to, że jeśli dana cyfra występuje w dwóch kolumnach to nie może występować w więcej niż jednym wierszu i odwrotnie, jeśli występuje w co najmniej dwóch wierszach to nie może występować w więcej niż jednej kolumnie. Inaczej mówiąc, jeśli dana cyfra jest w diagramie wpisana kilka razy to wszystkie jej wystąpienia muszą być albo w tej samej kolumnie albo w tym samym wierszu.
Rozumiem, ale to nie TO.
mp
jeśli w diagramie występują takie same cyfry, to stoją obok siebie
Czyżby liczba wskazywała liczbę liczb w wierszu i kolumnie, w której ta liczba stoi (nie licząc tej liczby)?
😀
Fanfary!
mp
Hmmm…. Jak odkryłem regułę, to zadanie pękło w minutę, dosłownie!
5_____
5_____
055676
6___3_
6___3_
7__3_3
p.s. ‚0’ oznacza 10, aby się diagram nie rozwalił.
Wszystkie liczby użyte w diagramie, po ustawieniu od najmniejszej do największej, tworzą ciąg arytmetyczny o różnicy 1.
Nie tędy droga.
mp
PS już dwie osoby (do środowego poranka) odgadły warunek
suma liczb w każdym spójnym fragmencie jest kwadratem liczby całkowitej
Oj, nie – nie aż tak! Jak rozwiązywać przy takim warunku – bo to i spójność, i kwadrat.
mp
hmm, no to może ilość liczb w każdym ze spójnych obszarów wyrażona jest liczbą pierwszą większą od 1 🙂
Liczba wpisana w daną kratkę jest równa liczbie niepustych kratek znajdujących się w tym samym wierszu i kolumnie co dana kratka (nie wliczając jej samej).
Przy takim warunku, droga do rozwiązania faktycznie wiedzie jak po sznurku.
Można i tak 🙂 (bo u mnie są liczby zamiast niepustych kratek).
mp
Jest jeszcze kilka rozwiązań, stud, np.:
0 2 0 0,
0 0 2 0,
0 0 0 1,
9 1 1 4.
1 1 0 0,
0 0 2 0,
0 0 0 1,
8 2 1 4.
1 1 0 0,
0 0 1 1,
0 0 0 1,
8 2 2 3. itp.
@budfy
Trzy liczby są zadane na początku.
@budfy: zakładam, że trzy cyfry wpisane w przykładzie są „nie do ruszenia”
Czy chodzi o to aby wpisanych liczb było ich jak najmniej ?
Nie.
mp
najmniej udało mi się dopisać 9 liczb ale niestety można to zrobić na kilka sposobów. może wpisywane liczby mają się trzymać brzegów diagramu ?
No ale jak to do Omnibusa, to warunek powinien być w miarę prosty… Patrzę na Diagramy Studa i najprostsze co się narzuca, to pojawienie się liczby 5. To jest bok kwadratu (4) plus 1. W moim kilka wpisów wyżej rozwiązaniu zadania 6×6 pojawia się cyfra 7 i jak się ją w lewym dolnym rogu wpisze (podobnie jak 5 w 4×4), to zadanie robi się samo.
w rozwiązaniu występują kolejne liczby
Liczby uzupełniamy wierszami albo kolumnami zaczynając od lewego górnego rogu wpisując za każdym razem maksymalną możliwą liczbę.
5
5
10 5 5 9 7 3
6 3
6 3
7 6
rozwiązanie zostało skrzywione przez edytor
ma być tak:
5
5
10 5 5 9 7 3
6———–3
6———–3
7————–6
jak wyjdziemy z lewego dolnego rogu to rozwiązanie jest inne ale też jednakowe dla poruszania się wierszami jak i kolumnami.
jak wyjdziemy z prawego dolnego to rozwiązania nie ma ani dla wierszy ani dla kolumn.
prawy górny wierszami i kolumnami daje to samo co lewy dolny
można by jeszcze rozważać poruszanie się zygzakiem albo spiralą albo….
i już mamy materiał na nową teorię 🙂
Hmm, uwolnione czyli nie to ???
No, ale ta reguła daje jednoznaczne rozwiązanie :/
Konsternacja 😉
Reguł, które dadzą jednoznaczne rozwiązanie (w podanym konkretnym przykładzie), można znaleźć wiele. TA, czyli prosta, elegancka, uniwersalna – no i „autorska” – jest tylko jedna.
mp
No to jeszcze tak można, że idziemy od lewej, i w lewej kolumnie musi być max tam gdzie się da (albo lepiej: idąc od góry). Czyli jeśli da się, by pod dwójką była dwójka, to wpisujemy. W trzecim wierszu nic się już nie da, w czwartym wpisujemy 5, i rozwiązujemy dalej, jest już jednoznacznie. W przykładzie 6×6 piszemy pod 5 drugie 5 i dalej 6 koło 9 i drugie 6, a w ostatnim rzędzie 7. Potem max co się da koło 10 postawić to jest 5. Potem jeszcze jedno 5 w tym rzędzie. Potem w tym samym rzędzie 9, dalej 7 i zostaje 3, a więc w prawym dolnym rogu zostaje 6. Algorytm jest jasny i jednoznaczny, ale to pewnie nie to 🙂 Łatwiej rozwiązać zadanie, niż odgadnąć czyjeś myśli.
Można i tak, ale chodzi o prostą regułę, którą można przedstawić w jednym niedługim zdaniu, zaczynającym się od:
„Każda liczba wpisana w diagram powinna być równa…” (to jest spora podpowiedź).
mp
Jestem ogromnie ciekawy, czy po prawie dwóch tygodniach dołączył ktoś do nas dwóch (mam na myśli szczęśliwców, którzy wpadli na regułę), bo…
nieźle Pan przeciąga czas pomiędzy wpisami 🙂
Dotąd na regułę wpadły trzy osoby.
Przyczyną przeciągania czasu jest brak czasu.
mp
Każda liczba wpisana w diagram powinna być równa sumie liczb: najmniejszej liczby z kolumny w której się znajduje oraz najmniejszej liczby z wiersza w którym się znajduje;
jeśli ową najmniejszą z kolumny i najmniejszą z wiersza jest właśnie rozpatrywana liczba to nie sumujemy jej z samą sobą 🙂
troche zagmatwane…
więc bardziej przejrzyście:
1. dla każdej kolumny i każdego wiersza wyznaczamy wartość najmniejszą;
2. na przecięciu danego wiersza z daną kolumną dla których wartości najmniejsze są równe wpisujemy właśnie tę wartość lub komórke pozostawiamy pustą;
3. na przecięciu danego wiersza z daną kolumną dla których wartości najmniejsze są różne wpisujemy ich sumę lub komórkę pozostawiamy pustą.
liczbie niezerowych pól w danym wierszu i kolumnie, z pominięciem tejże liczby.
500000
500000
1055676
600030
600030
700303
Ciekawe, że rozumując inaczej, doszedłem do poprawnego rozwiązania, ale tego o które chodziło, przyznam się szczerze, nie wymyśliłem. W ogóle nie w tę stronę kombinowałem. Łamiblog uczy pokory 🙂