Tripolis
Jak nazwać miasto, które ma kształt trójkąta, a układ ulic tworzy trójkątną sieć? Podchodzi mi określenie Tripolis, choć nie jest jednoznaczne, ponieważ równie, a nawet bardziej pasuje ono jako synonim trójmiasta.
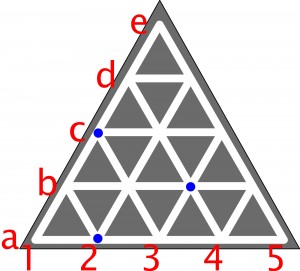
Oto małe Tripolis z oznaczoną siecią ulic:
Na trzech skrzyżowaniach (a2, b3, c1) umieszczone są kamery policyjne. Tyle wystarczy, aby wszystkie skrzyżowania były przez władzę obserwowane.
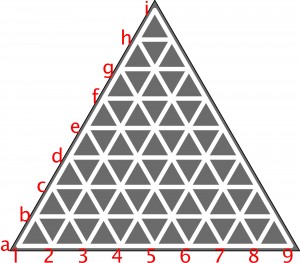
Kolej na inne, większe Tripolis; albo to samo, ale po stu latach:
Na ilu co najmniej skrzyżowaniach i na których należy w tym mieście ustawić kamery, aby miały one oko na wszystkie 45 skrzyżowań? Inaczej mówiąc, z każdego skrzyżowania powinna być widziana przynajmniej jedna kamera. Zakładamy oczywiście, że kamera może obserwować także skrzyżowanie, na którym się znajduje.

Komentarze
Na pierwszy rzut oka znajduję rozwiązanie z pięcioma kamerami. Można je umieścić na wiele sposobów, np.: A1, B2, C3, D4, E5
Domyślam się, że wystarczy mniej kamer… zatem szukamy dalej…
Na drugi rzut oka znalazłem następujące rozwiązanie: A9, B5, D1, F3
http://www.gg.pl/dysk/lwSSZ7uVKb9QlgSSZ7uVOZY/tripolis.jpg
Oczywiście to jedno rozwiązanie generuje 5 innych poprzez zastosowanie jednego z automorfizmów naszego miasta.
i1 e2 c6 a4
plus 5 symetrycznych rozwiązań
Czy narożniki to też skrzyżowania? wg mnie na 100% wystarczą 4 kamery ale póki co rozwiązania brak.
Narożnik=skrzyżowanie (powinienem ciutek poprzedłużać ulice :))
mp
PS byłoby ciekawie, gdyby ktoś opisał metodę rozwiązywania. Moim zdaniem rozwiązanie jest tylko jedno (z dokładnością do obrotów i odbić)
kamera stojąca poza ulicą nadbrzeżną miasta obserwuje na niej co najwyżej 2 skrzyżowania. Trójkąt ma bok 9. Jeśli mają wystarczyć 4 kamery, na każdej krawędzi miasta musi stać kamera.
a) jeśli kamera stoi w wierzchołku trójkąta, to nie ma sensu stawiać jej w innym wierzchołku. Czyli, uwzględniając symetrię, rozwiązań wystarczy szukać, stawiając kamerę w górnym wierzchołku i w a2 lub a3 lub a4 lub a5.
b) gdyby żadna kamera nie stała w wierzchołku, aż 3 kamery musiałyby stać na 3 różnych brzegach miasta. Rozpatrzmy wewnętrzny trójkąt o rozmiarze 6. Żaden jego boków nie jest w pełni obserwowany przez 3 kamery z brzegu miasta patrzące „z boku”, bo te kamery „z boku” widzą tylko 1 skrzyżowanie. Pozostała, 4. kamera nie może uzupełnić tego braku. Więc co najmniej 2 kamery muszą stać w a2, h2, b7. Szybko można stwierdzić, że w tym przypadku nie ma rozwiązań. Wracamy do wariantu a)
Jeżeli wiemy, że jedną kamerę należy ustawić w wierzchołku, to zagadnienie redukujemy do problemu „ustawić 3 kamery w tripolisie o rozmiarze 7”. Rozumując analogicznie widzimy, że co najmniej 2 z tych kamer muszą stać na jego brzegach. Łatwo zauważyć, że żadna nie może stać w jego wierzchołku (bo wtedy 2 kamery kontrolowałyby tripolis o boku 5), więc 3 kamery stoją na bokach wewnętrznego tripolis o boku 7. To już dość potężna wskazówka.
Komputer potwierdził, że istnieje tylko 6 rozwiązań. Jedno z nich podałem wczoraj, pozostałe powstają przez odbicie symetryczne i/lub obroty.
Przyznam, że rozwiązanie znalazłem ręcznie przez przypadek, więc ciężko mi opisać sposób jego uzyskania.
Można umieścić 4 kamery na skrzyżowaniach: a6, c /2, e /4, i /1.
Pozdrawiam 😉
A1,B6,D2,F4.
Potwierdzam, że z dokładnością do obrotów i odbić, jest to jedyne rozwiązanie (sprawdzone komputerowo 🙂 ).
Dla Tripolis o jeden stopień mniejszego (z 36 skrzyżowaniami), również potrzeba 4 kamer.
Trzy kamery wystarczą do obserwacji w Tripolis o 2 stopnie mniejszym (z 28 skrzyżowaniami).
a4, c7, e4, i5
Może niedokładnie opisałam położenie. Inaczej : a4, c68, e26, i19.
Oba zapisy są nietypowe, choć łatwo się zorientować w czym rzecz i rozwiązanie jest poprawne.
Właściwy zapis: a4, c6, e2, i1 (litera oznacza rząd, cyfra – kolejne skrzyżowanie w danym rzędzie).
mp
Tripolis o rozmiarze 8 można załatwić trzema kamerami umieszczonymi na trzech bokach miasta – każda w odległości dwóch skrzyżowań od któregoś wierzchołka.
W Tripolis o rozmiarze 9 umieszczenie kamery w narożniku sprowadza problem do powyższego.
Jest jedno rozwiązanie z dokładnością do odbić i obrotów:
1,1
2,4
4,6
6,2
Jeśli dopuścimy, że każde skrzyżowanie jest „inne” to mamy 6 rozwiązań otrzymanych z powyższego przez obroty trójkąta o 60 stopni i odbicia względem wysokości. 🙂
5 kamerkami nie ma problemu, jest mnóstwo rozwiązań,
Doszedłem jednak do wniosku, że 4 kamerkami się nie da.
Dowód: Spójrzmy np. na skrzyżowania na dolnej krawędź trójkąta, jeśli nie będzie na niej żadnej kamerki to jedno skrzyżowanie na pewno nie zostanie obstawione, gdyż każda kamerka widzi dwa z nich.
Postawmy więc kamerkę na dolnej krawędzi (gdziekolwiek poza wierzchołkiem trójkąta), obstawimy wówczas dwa skrzyżowania lewej krawędzi, 7 pozostaje nieobstawionych, więc trzy kamerki to za mało, no chyba, że jedna z nich będzie na lewej krawędzi. Ale wtedy na prawej krawędzi pozostanie nam do obstawienia 5 skrzyżowań mając dwie kamerki do dyspozycji. Więc znowu kamerka musiałaby być na krawędzi. Wtedy pozostanie nam jedna wolna kamerka, którą w żaden sposób nie pokryjemy pozostałych skrzyżowań.
Postawmy więc jedną kamerkę na wierzchołku trójkąta. Niech będzie to górny wierzchołek. Boczne krawędzie mamy załatwione, jednak na dolnej pozostaje 7 skrzyżowań, mamy tylko trzy kamerki więc jedna z nich musi być na tejże właśnie krawędzi. Pozostają nam dwie kamerki i układ skrzyżowań taki, że nie sposób ich obstawić tylko dwoma kamerkami. W tym miejscu dowód się urywa ale jestem na 99% pewien, że nie sposób to rozwiązać. Zapewne właśnie ten 1% to to jedno rozwiązanie o którym pisze gospodarz 😉
Ciekawe jak te minimalne układy wyglądają dla kolejnych n ???
Mając rozwiązanie dla n=9 można łatwo dostrzec rozmieszczenie 3 kamer dla n=8.
W rozwiązaniu, które podałem wcześniej, dla pierwszych współrzędnych jest oczywiście a=1, b=2 i.t.d….
Poniżej link do programu, który w kilkanaście sekund oblicza rozwiązanie:
http://pokazywarka.pl/62y9zs/
Da się obstawić ten trójkąt 4 kamerkami.
Dowód: przedostatni wpis Rubika ma numer 190017, a ostatni – 190026. Oznacza to, że jest tam 8 nieujawnionych wpisów z dobrymi odpowiedziami. Plus 2 dobre między Miodziem a Rubikiem. 😉
A jednak się da… http://bankfotek.pl/view/1849859
Metodologia taka jak w moim „dowodzie” 😉
Musi być kamerka na wierzchołku i na przeciwległej do niego krawędzi. Pozostałe dwie kamerki metoda prób i błędów.
Łatwo zauważyć, że skrzyzowań na brzegach jest 9, kamera potrafi na jeden ‚brzeg’ rzucic dwa promienie. Przy 4 kamerach mamy ‚obstawione’ tylko 8 skrzyżowań, a więc jedna z tych kamer powinna stać na brzegu miasta, co obstawi nam to 9 skrzyżowanie.
Ponieważ miasto jest trójkątne (nie wdając się w głębsze przemyślenia) kamera powinna stać na ostrzu trójkąta, wyeliminuje to nam dwa brzegi 9-skrzyzowaniowe, pozostawiając trzeci brzeg miasta z 7 skrzyżowaniami. Rozumując podobnie (3 kamery, 7 skrzyzowań => kamera musi byc na linii) i delikatnie zgadując, można dość szybko dojść do układu z 4 kamerami.
http://postimg.org/image/ms46x9lgh/
P.S. Przy okazji mamy rozwiązane podobne zadanie dla 3 kamer i miasta z bokiem z 7 skrzyzowaniami.
P.P.S. w tym przypadku cieszę się, że wpisy pojawiają sie rzadziej… mogłem ugryźć to zadanie zaglądając tu raz na tyle dni 🙂 choć mam lekko mieszane uczucia, czy to wystarczający argument na taką częstotliwość pojawiania sie wpisów 🙂
Możliwe, że to wynik jakiejś pandemii braku czasu obejmującej, na szczęście, tak duży obszar Polski, od gór po pojezierze 😉
Oczywiście napisałem głupotę, ale z dobrymi intencjami 😉 W pierwszym zdaniu miało być „Tripolis o rozmiarze 7”.
@y-b: Tak, tak, ja też walnąłem tego byka, ale już nie prostowałem, bo wiadomo o co chodzi. Prawnicy mówią na coś takiego „oczywista pomyłka” 😉