Wagoniki bis
Jestem pod urokiem Wagoników z poprzedniego wpisu, więc jeszcze przez chwilę będę się ich trzymał.
Pomysł tego zadania ma sporo wspólnego z przebojową, znaną od lat 90. łamigłówką-przesuwanką Rush Hour, która dostępna jest także w Polsce. Pisałem już o niej kiedyś, więc tylko przypomnę, że chodzi o „uwolnienie” małego czerwonego samochodziku, czyli wyjechanie nim z zastawionego autami parkingu. Kłopot w tym, że jest tylko jeden wąski wyjazd i dotrzeć doń należy czerwonym maluchem, manewrując odpowiednio pozostałymi pojazdami, czyli przesuwając je wielokrotnie w odpowiedniej kolejności – oczywiście każdy tylko do przodu i do tyłu. Poniżej pokazana jest przykładowa łamigłówka – „w realu” i schematycznie.
Wagoniki są jakby statyczną wersją Rush Hour, tzn. rozwiązanie polega na odtworzeniu rozmieszczenia pojazdów, które można by uznać za sytuację wyjściową w przesuwance. Auta w Rush Hour także mają, podobnie jak wagoniki, „stopnie swobody”, które jednak zmieniają się w trakcie rozwiązywania.
Zrobiłem wnikliwą kwerendę w poszukiwaniu źródeł Wagoników. Wydaje się prawie pewne, że oparte są właśnie na Rush Hour. Pierwsze tego typu zadanie pojawiło się bowiem w roku 2006 na łamigłówkowych mistrzostwach Japonii (Rush Hour także ma japoński rodowód) i nazywało się po prostu Parking.
Zamieszczona poniżej łamigłówka z łamów tureckiego pisma Akil oyunlari różni się dwoma szczegółami od japońskiego oryginału (stopnie swobody nie wszystkich wagoników są ujawnione oraz wymagana jest spójność wolnych pól).
Przypominam zasady.
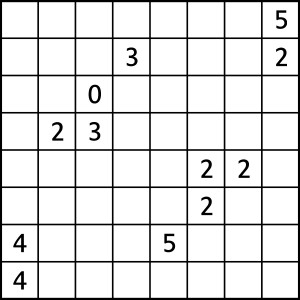
Na diagramie należy rozmieścić wagoniki 1×2 i 1×3. Każde pole z liczbą powinien objąć jakiś wagonik (jeden wagonik – tylko jedna liczbę), ale nie każdy wagon musi obejmować pole z liczbą. Jeśli obejmuje, to powinien mieć tyle stopni swobody, jaka jest wartość liczby. Liczba stopni swobody równa jest łącznej liczbie wolnych pól przed i za wagonikiem. Pola nie zajęte przez wagoniki powinny tworzyć jeden spójny obszar.
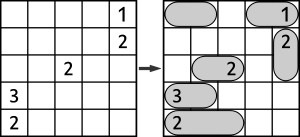
Przykład:
Zadanie:



Komentarze
xxxxx555
x333xx22
x200-xxx
x23–22x
423–22x
4xx2222x
4xx55xxx
44xxxx–
Cyfry oznaczają liczbę stopni swobody danego wagonika,
x to wolne pole, – identyfikuje wagoniki bez podanych stopni swobody.
Granice wagoników łatwo z powyższego wydedukować samodzielnie.
http://i.imgur.com/ve7IRqE.png
W kupie siła! Kupy nikt nie ruszy!
~~~~~555
~333~~22
~200X~~~
~23YX22~
423YX22~
4~~2222~
4~~55~~~
44~~~~ZZ
Oto rozwiązanie: http://www.gg.pl/dysk/d6a5bC4unqJQdqa5bC4ujos/wagoniki.png
Voila!
http://pokazywarka.pl/ad5nwp/
Nie wiem, czy za bardzo nie przekombinowałem. Ten podwójny wagonik w centralnej części diagramu służy tylko jako „zapychacz” aby wolne od wagoników pole pozostało spójne.
http://bankfotek.pl/image/1749234
wakacje?
Tak, przerwa na odsapkę 🙂
mp
Czyżby przerwa?
a
Właśnie po dłuższym czasie zerknąłem do Łamibloga i…. nie tylko ja miałem przerwę 🙂 Cieszę się, że nic nie straciłem:)
Na razie nie ma co się przejmować przerwą w Łamiblogu. Właśnie ukazał się „Omnibus – wakacyjny”, więc będzie co robić przez wiele dni.
Panie Marku, długa ta przerwa się robi:) mam nadzieję, że to tylko urlop!
Nawrócę się za tydzień
mp
‚nawrócę’?? ja tu myślałem, że nie-daj-Boże choroba jaka zmogła, a tu ‚nawrócę’? Do klasztoru jakiegoś chyba Pan się nie zamknął, bo by z internetu korzystać pewnie zabronili 😉
Wiązie, klasztory mają swoje strony w internecie, mój także – Czerwony Klasztor w Pieninach 🙂
mp
Jeżeli chcecie „powalczyć” z innymi łamigłówkami autorstwa Gospodarza, to w każdą sobotę ukazuje się dodatek do Wyborczej „na pamięć”. W ostatnim było 10 różnych, ciekawych zadań Marka. Innych łamigłówek też mnóstwo. Polecam.