Przepychanki
Wpisy w Łamiblogu pojawiają się rzadziej niż dawniej (brak czasu), więc zadania bywają trudniejsze – takie bardziej dla wytrwałych, dla programistów albo dla wytrwałych programistów. Dziś postanowiłem trochę przegiąć i rzucić wyzwanie najwytrwalszym, zamieszczając rodzaj zadania, za którym nie przepadam, czyli przesuwankę.
Kwadrat ułożony z płytek przypominających skrablowe, ale z cyframi, jaki jest, każdy widzi.
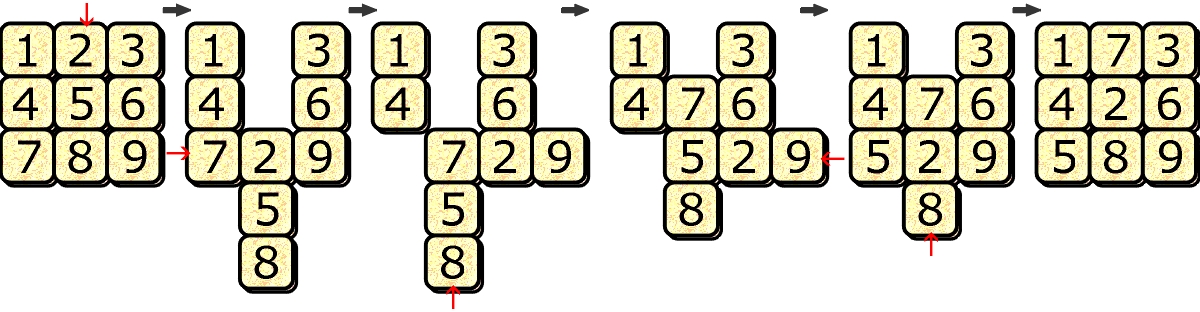
Jedyny dozwolony ruch to przepychanie rzędu złożonego z trzech płytek – w dół (D), w górę (G), w lewo (L) lub w prawo (P). W ten sposób można zmieniać układ płytek. Co można zrobić w pięciu ruchach, pokazuje przykład:
Zapis tego przemeblowania wygląda tak:
2DD-7P-8G-9L-8G.
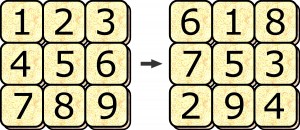
Zadanie polega na wykonaniu przepychanki złożonej z jak najmniejszej liczby ruchów, która zmieni układ wyjściowy w kwadrat magiczny, czyli:
Szkopuł w tym, że kwadrat magiczny nie musi znajdować się w takiej pozycji jak na rysunku – może być w jednym z ośmiu możliwych ustawień (obroty i odbicia lustrzane). A szkopuł szkopułu w tym, że niektóre z tych ustawień są w ogóle niemożliwe do uzyskania dozwolonym sposobem przepychania.
Czy ktoś się pokusi o znalezienie najlepszego, czyli najkrótszego rozwiązania (którego nie znam; wiem tylko, że podobno można zejść poniżej 20 ruchów)? Mam nadzieję, że tak.


Komentarze
No, Panie Marku, pojechał Pan po bandzie:
dla wytrwałych: OK,
dla programistów: no, jeszcze OK,
ale dla wytrwałych programistów?!
Domyślam się, że pchnięcie o dwa pola liczymy tak samo jak o jedno pole, czyli w obu przypadkach zaliczamy jeden ruch ?
Tak
mp
Ile ruchów ma znane Panu rozwiązanie ?
Nie znam (na razie) żadnego konkretnego rozwiązania.
mp
Gdyby ruchy wykonywać w układzie z periodycznymi warunkami brzegowymi, kwadrat magiczny
429
753
186
można by osiągnąć w zaledwie 2 ruchach.
Co więcej, w układzie z periodycznymi warunkami brzegowymi istnieje dokładnie 181440 ustawień planszy, które można osiągnąć z ustawienia początkowego, co ilustruje tabelka:
i = 0, 1
i = 1, 13
i = 2, 109
i = 3, 845
i = 4, 6053
i = 5, 34727
i = 6, 124224
i = 7, 178965
i = 8, 181440
gdzie i to liczba ruchów, a druga liczba to liczba możliwych konfiguracji po 0,1,…, i ruchach (kumulatywnie).
Z kolei 9! = 362880, czyli liczba dostępnych stanów = 9!/2.
I wszystko jasne, permutacja odpowiadająca periodycznemu przesunięciu dowolnego
wiersza/kolumny jest parzysta, stąd 2 w mianowniku i uwaga Gospodarza, że nie każda konfiguracja końcowa jest osiągalna.
Zwracam uwagę, że każdemu ruchowi w grze odpowiada ruch w układzie z periodycznymi brzegami ale nie odwrotnie, niestety.
Ta obserwacja dowodzi jednak, że nie każdy stan w grze z otwartymi brzegami jest osiągalny.
Prawdopodobnie te uwagi nie zbliżają nas do rozwiązania, ale może kogoś zainteresują. Mam nadzieję, że nikogo nie zawiodą na manowce.
Kwadrat magiczny na początku jest nie do końca magiczny.
Warto by wyjaśnić znaczenie pojęcia „periodyczne warunki brzegowe”.
mp
„Periodyczne warunki brzegowe” rozumiem, że kwadrat (plansza) jest torusem czyli oponką, jak cyfra znika z prawej to zaraz pojawia się z lewej na opróżnionym polu. Odpowiednio znika na dole pojawia się na górze.
Miałem błąd w weryfikacji magiczności w pionie. Do utworzenia kwadratu magicznego z periodycznymi warunkami brzegowymi potrzebne są nie 2, a 4 ruchy. Można w ten sposób utworzyć 4 z 8 kwadratów magicznych. Te 4 dozwolone kwadraty odpowiadają permutacjom parzystym, oczywiście, a 4 niedozwolone – nieparzystym. Układ na rysunku to permutacja nieparzysta, jest więc nieosiągalny (no i mały podstęp Gospodarza się wydał). Wystarczy go odbić w pionie/poziomie (permutacja nieparzysta), by uzyskać kwadrat magiczny dozwolony. Obroty to permutacje parzyste, więc obrót kwadratu dozwolonego przeprowadza go w inny kwadrat dozwolony.
Układ z periodycznymi warunkami brzegowymi to taki układ, w którym współrzędne x i y liczy się modulo 3. Innymi słowy, jeżeli wypchnę kostkę poza kwadrat (przy pchnięciu o jedno pole), to muszę wypchniętą kostkę wstawić na wolne miejsce, a pchnięcia o N>1 definiuje się przez złożenie pchnięć o 1 pole. Np wiersz 123 można w ten sposób zamienić tylko na 231 lub 312, pchnięcie o 3 przeprowadza wiersz/kolumnę/kwadrat na siebie. To założenie upraszcza geometrię: zawsze pracujemy na kwadracie a nie jakimś niekształtnym zwierzątku.
Kwadrat magiczny da się uzyskać w 11 krokach, np.:
2DD-9L-8GG-3LL-2G-1PP-6LL-3DD-7P-2PP-6G
3L-4P-3D-9LL-6LL-1DD-2DD-7PPP-8G-2LL-6DD
7G-9GG-9L-7GG-8GG-3LL-6LL-1DDD-4P-6GG-8LL
9LL-9G-3LL-6LL-1DDD-7P-6G-2DD-1L-7G-4D
1PP-9GG-3L-1DDD-4PP-7PP-8GG-2GG-9P-3DD-4D
1P-2D-4PP-7PP-9GG-8GG-1P-3DD-2LL-4D-9PP
9L-1D-7PP-3D-9L-6G-3L-2DD-8G-1P-6D
6LL-7G-4PP-8GG-3L-2DD-1DD-9LL-7LL-4G-2L
7G-2D-7P-8GG-3D-6L-9GGG-4PP-1PP-6D-8PP
7PP-3DD-9L-7GGG-1PP-4PP-2DD-8DD-3P-6DD-8D
1D-9L-7G-2DD-4P-9G-8P-3D-6LL-1D-8P
9G-1P-4PP-3DD-7PP-9LL-4G-2LL-8GG-6L-1DD
2DD-7P-8GG-4PP-3D-6LL-9LL-7DD-1DD-8P-6D
W pliku http://www.gg.pl/dysk/qGvVFeMVpBZQqWvVFeMVtD8/sol.zip umieszczam wszystkie znalezione sekwencje ruchów, które w 11 lub 12 krokach uzyskują kwadrat magiczny. Jest ich około 1700 (w tym nieco ponad 100 w 11 krokach, pozostałe w 12).
Pięknie i szybko. Gratulacje!
mp
A ja mam założenie – nie wiem czy słuszne, że figura musi pozostać „spójna” (kostki muszą stykać się co najmniej rogami. Przykładowo sekwencja 1PP – 1 DD jest niedopuszczalna.
Proszę o potwierdzenie mojego założenia 🙂
4P – 8G – 1P – 2D – 6L – 7P – 4D – 1P – 8GG – 2L – 4D – 8L – 2D – 7P – 6G
Czy ktoś mógłby to sprawdzić? (W tej notacji łatwo o pomyłkę).
Moim zdaniem coś tu nie gra.
mp
Przy założeniu, że pojedynczy ruch może przesunąć blok tylko o jedną kratkę, minimalną liczbą ruchów jest 13. Istnieje 16 sekwencji składających się z 13 ruchów, które przekształcają wyjściowy kwadrat w kwadrat magiczny:
3L-7G-1P-1P-9G-3L-6D-9L-2D-8G-8G-7P-6G
7P-3D-9L-4P-4P-8G-3L-6G-1P-2D-2D-7P-6G
1P-9G-3L-4P-4P-2D-9L-6D-7P-8G-8G-1P-6D
9L-1D-7P-7P-3D-9L-6G-3L-8G-2D-2D-1P-6D
7G-3L-1D-1D-9L-7G-8P-9G-6L-6L-4P-3D-8L
3D-7P-2D-2D-9G-6L-7G-8L-1D-4P-4P-3D-8L
3D-7P-9G-9G-1P-3D-2L-1D-4P-4P-6L-7G-2P
7G-3L-8G-8G-1D-4P-3D-2P-9G-6L-6L-7G-2P
3L-7G-1P-6L-6L-2D-7P-4D-9L-8G-8G-3L-4D
7P-3D-9L-9L-1D-7P-4G-1P-8G-2D-2D-3L-4D
1D-9L-2D-2D-7G-4P-9G-8P-3D-6L-6L-1D-8P
9G-1P-3D-3D-7P-9G-8L-7G-6L-4P-4P-1D-8P
9G-1P-8G-8G-3D-6L-1D-2L-7G-4P-4P-9G-2L
1D-9L-7G-7G-3L-1D-2P-3D-6L-6L-4P-9G-2L
9L-1D-6L-6L-7P-8G-1P-4G-3L-2D-2D-9L-4G
1P-9G-3L-3L-7G-1P-4D-7P-2D-8G-8G-9L-4G
Teraz dopiero zauważyłem, że wszystkie przesłane przed chwilą rozwiązania minimalizujące sumaryczną długość przesunięć, są de facto rozwiązaniami optymalnymi w oryginalnym zadaniu.
Zatem poniższe rozwiązania są minimalne zarówno pod względem liczby ruchów w oryginalnym zadaniu (11 ruchów) jak i pod względem sumarycznej odległości przebytej przez płytki (13).
3L-7G-1PP-9G-3L-6D-9L-2D-8GG-7P-6G
7P-3D-9L-4PP-8G-3L-6G-1P-2DD-7P-6G
1P-9G-3L-4PP-2D-9L-6D-7P-8GG-1P-6D
9L-1D-7PP-3D-9L-6G-3L-8G-2DD-1P-6D
7G-3L-1DD-9L-7G-8P-9G-6LL-4P-3D-8L
3D-7P-2DD-9G-6L-7G-8L-1D-4PP-3D-8L
3D-7P-9GG-1P-3D-2L-1D-4PP-6L-7G-2P
7G-3L-8GG-1D-4P-3D-2P-9G-6LL-7G-2P
3L-7G-1P-6LL-2D-7P-4D-9L-8GG-3L-4D
7P-3D-9LL-1D-7P-4G-1P-8G-2DD-3L-4D
1D-9L-2DD-7G-4P-9G-8P-3D-6LL-1D-8P
9G-1P-3DD-7P-9G-8L-7G-6L-4PP-1D-8P
9G-1P-8GG-3D-6L-1D-2L-7G-4PP-9G-2L
1D-9L-7GG-3L-1D-2P-3D-6LL-4P-9G-2L
9L-1D-6LL-7P-8G-1P-4G-3L-2DD-9L-4G
1P-9G-3LL-7G-1P-4D-7P-2D-8GG-9L-4G
4P – 8G – 1P – 2D – 6L – 7P – 4D – 9L – 8GG – 3L – 4D – 8L – 2D – 7P – 6G
powstaje kwadrat
294
753
618
Poniżej rozwiązanie w wersji w jakiej wyprodukował je komputer. Czyta się je od dołu (BEGIN).
Układ cyfr w układzie, w którym 5 jest zawsze w środku.
Cyfry, które wychodzą poza kwadrat 3×3 z cyfrą 5 w środku kodowane są jako litery, a=A=1, b=B=2, c=C=3 etc.
Małe litery: cyfra wyszła poza kwadrat na lewo lub do góry.
Duże litery: cyfra wyszła poza kwadrat na prawo lub na dół
(oś „y” w dół, punkt (0,0) w lewym górnym rogu umownego kwadratu).
Niektóre ruchy opatrzone są komentarzem SKIP! i te człowiek pomija, bo mogą być z łozone z innym ruchem w jeden. Np 8GG tp dwa ruch 8G i pierwszy ma komentarz SKIP! Podobnie komputer nigdy nie przesuwa środkowego wiersza i kolumny (dlatego zawsze widzi 5 w środku kwadratu) i taki ruch symulowany jest poprzez przeciwny ruch dwóch pozostałych wierszy lub kolumn. Np. zamiast ruszyć środkowy wiersz w lewo komputer rusza 1. i 3. wiersz w prawo, a człowiek musi potem odpowiednio zinterpretować te ruchy i zamienic np. 1P-7P
na 6L. Mam nadzieję, że to jest zrozumiałe.
— KONIEC —
294
753
618
— 6G —
F94
253
718
— 7P —
F94
253
18g
— 2D —
294
153
68g
— 8L —
294
153
768
— 4D —
293
158
76d
— 3L —
C29
158
76d
— 8GG (= 8G + 8G) —
C24
159
768
— SKIP! (8G) —
C2H
154
769
— 9L —
C2H
154
I76
— 4D —
C24
156
I78
— 7P —
C24
156
789
— 6L (= 1P + 7P) —
C24
156
89g
— SKIP! (1P) —
243
156
89g
— 2D —
143
856
b9g
— 1P —
43a
856
b9g
— 8G —
23a
456
89g
— 4P (=3L + 9L) —
23a
456
789
— SKIP! (3L) —
123
456
789
— BEGIN —
Ponieważ mój program operuje na przesunięciach elementarnych (o 1 pole) i przesunięcia środkowych wierszy / kolumn symuluje jako przesunięcia 2 sąsiednich wierszy / kolumn, nie mam gwarancji, że nie istnieje krótsze rozwiązanie (np. mające więcej
pchnięć podwójnych), chociaż 15 ruchów wydaje się niezłym osiągnięciem.
3L – 7G – 1PP – 9G – 3L – 8G – 1P – 6DD – 9L – 8GG – 3L – 2D – 7P – 6G
14 ruchów, po drodze figura traci spójność
Miodziu, gratulacje!
Nie zauważyłem, że jeżeli chcę symulować ruch środkowego rzędu ruchem sąsiednich, nie mogę uzależniać możliwości wykonania ruchu w rzędzie centralnym od możliwości wykonania 2 ruchów w bocznych rzędach (co rzadko kiedy ma miejsce), dlatego moje rozwiązania są dość długie.