Łaciński łaciaty

17 kwietnia 2014
Marek Penszko

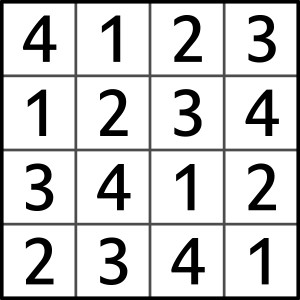
Jeśli zadanie polega na wypełnieniu pól kwadratu n×n cyframi od 1 do n tak, aby w każdym wierszu i w każdej kolumnie było n różnych cyfr, to efektem końcowym jest kwadrat łaciński, czyli dla n=4 np. taki:

Tak kończy się wiele łamigłówek, różniących się elementami, wyznaczającymi drogę do celu w taki sposób, aby rozwiązanie było tylko jedno. Tymi elementami mogą być np. ujawnione w diagramie cyfry (w sudoku), zależności między cyframi (w futoshiki) albo wyniki działań na dwóch lub więcej sąsiednich cyfrach (w kenken).

Jeśli natomiast do niektórych pól kwadratu n×n należy wpisać cyfry od 1 do m (m<n lub m=n) – nie powtarzając tej samej cyfry w żadnym wierszu i kolumnie – a pozostałe pola zaczernić, to powstanie kwadrat łaciński… „łaciaty”, na przykład taki:

W tym przypadku kluczem do rozwiązania są zwykle liczby podane przy brzegu diagramu. Powyższy łaciaty diagram stanowi więc rozwiązanie następującego zadania:

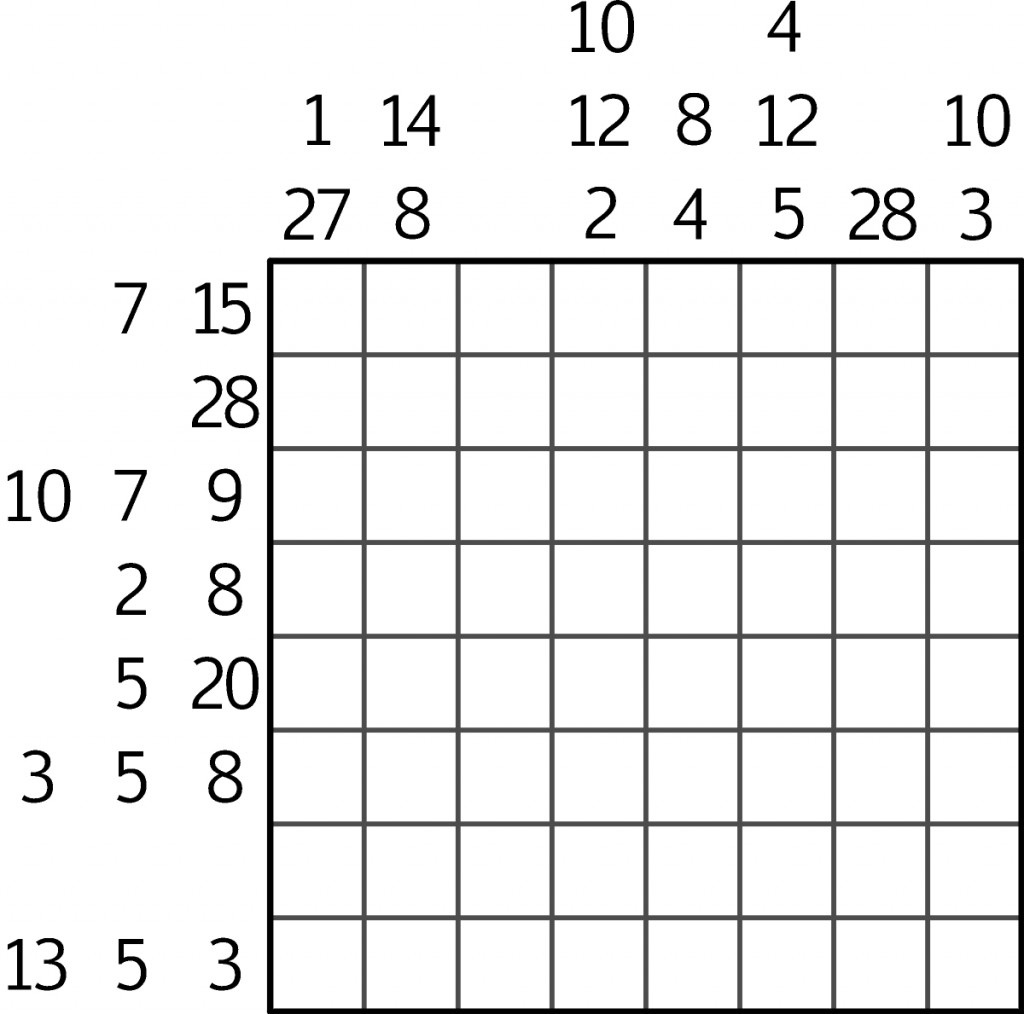
Nietrudno się zorientować, na czym polega „działanie” liczb przy brzegu: każda wyznacza sumę kolejnej grupy cyfr między czarnymi polami w danym rzędzie; grupy są także jednocyfrowe. Proponuję rozwiązać oparte na takiej zasadzie dość trudne zadanie, pochodzące z 18 Łamigłówkowych Mistrzostw Świata (Antalya, 2009):

W diagramie obok „łat” powinny pojawić się cyfry od 1 do 7. Brak liczb przed jednym wierszem i nad jedną kolumną jest tylko brakiem informacji, czyli nie oznacza, że w tych dwu rzędach nic się nie dzieje. W rozwiązaniu wystarczy podać sumę cyfr na przekątnych.