Krótki okres
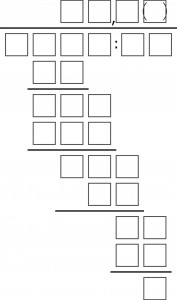
Wszystkie cyfry w zapisie dzielenia zastąpiono kratkami, czyli pozostał czysty „szkielet” działania. Dzielenie jest trochę nietypowe jak na arytmetykę szkieletową, bo iloraz zawiera ułamek okresowy, a okres jest jednocyfrowy – to cyfra w kratce z nawiasami.
Wiadomo o co chodzi – o rekonstrukcję, czyli praktycznie o wartość dzielnej i dzielnika. Początek jest niemal trywialny, bo kilka cyfr do wpisania to pewniaki. A dalej będzie pod górkę, ale niezbyt stromo. Miłej wspinaczki życzy kominiarz ;).

Komentarze
1060:75=14,1(3)
1078 : 12 = 89,8(3)
Dość szybko udało mi się znaleźć powyższe rozwiązanie, jednak nie do końca jestem przekonany, czy nie istnieją inne.
1078 / 12 = 89,8333…
Po wpisaniu dwóch oczywistych jedynek i dwóch zer wystarczy popatrzeć na końcówkę równania. Mamy tam [9][X] oraz [9-X][X]. Wystarczy znaleźć takie X, żeby te dwie liczby miały dwucyfrowy NWD.
1078:12=89,8(3)
Byłem przekonany, że rozwiązań jest więcej niż jedno a tu proszę 🙂
1078/12=89,8(3)
1078:12=89,83
Przyjemnie rekreacyjne 🙂
Jedyne rozwiązanie to:
1078 : 12 = 89,8(3)
znalezione programem mającym 26 linijek, bez grama dłubaniny ze sprawdzaniem układów cyfr 🙂
Dla koneserów podaję kod programu (w archaicznym basicu sprzed ćwierć wieku, gdzie nazwy plików nie mogą przekraczać 8 znaków)
dzielnik to: ef
wynik to: ab,c(d)
OPEN „krotkiok.txt” FOR OUTPUT AS #1
CLS
FOR c = 0 TO 9
FOR d = 1 TO 9
FOR e = 1 TO 9
FOR f = 0 TO 9
REDIM W(6)
IF (9 * c * f + 10 * d * e + d * f) MOD 90 = 0 THEN W(1) = 1
IF (c * (10 * e + f) 90) THEN W(2) = 1
IF (d * (10 * e + f) 9) THEN W(3) = 1
IF W(1) * W(2) * W(3) = 0 THEN GOTO skok
FOR a = 1 TO 9
FOR b = 0 TO 9
REDIM W(6)
IF (a * (10 * e + f) 9) THEN W(4) = 1
IF (b * (10 * e + f) 99) THEN W(5) = 1
IF ((10 * a + b + c / 10 + d / 90) * (10 * e + f) 999) THEN W(6) = 1
IF W(4) * W(5) * W(6) = 1 THEN WRITE #1, a, b, c, d, e, f, „*”, (10 * a + b + c / 10 + d / 90) * (10 * e + f), „/”, (10 * e + f)
NEXT b
NEXT a
skok:
NEXT f
NEXT e
NEXT d
NEXT c
CLOSE
No niestety ale ten edytor nie przepuszcza znaków „mniejsze/większe” więc program oczywiście jest do bani ale idea jest zarysowana.
1078:12
1078:12=89,8(3); to jedyne rozwiązanie. Zadanie robi się proste, jak się wpadnie na pomysł, mianowicie nie trzeba rozważać ogromnej liczby przypadków, tylko skupić się na parach (10*n, 9*n), gdzie n jest liczbą naturalną od 2 do 9. Ściśle biorąc, należy wziąć pod uwagę wszystkie dwucyfrowe dzielniki liczby 9*n, czyli np. dla n=8 będą to 72, 36, 24, 18 i 12. Szukany dzielnik musi się odznaczać taką właściwością, że ma wielokrotność pomiędzy 90 a 100, w dodatku różnica liczby 100 i tej wielokrotności jest równa n. I to już jest możliwe tylko dla jednego n, mianowicie n=4, dzielnikiem jest 12. I tak, od dołu do góry, sobie rekonstruujemy dalej – początek, czyli dzielna, wieńczy dzieło 🙂
1078 : 12 = 89,8(3)
1078/12=89,8(3)
Wynik uzyskałem bez użycia komputera, sprawdzając wpisy w okienka szablonu dla sześciu możliwych wartosci dzielnika, mając ustalone położenia kilku jedynek i zer.
1078:12 = 89,8(3)
@Spytko: stary dobry Basic; już myślałem, że nikt go nie używa, a tu taka niespodzianka 😀
P.S. Na wklejanie kodów polecam: http://www.ideone.com
o rzesz.. Basica widziałem ostatni raz w szkole… podstawowej 🙂
Jakoś nie odczuwam potrzeby przechodzenia na nowsze narzędzia programowania. Najważniejszy jest pomysł algorytmu a język to sprawa drugorzędna. Jednak pierwszym językiem z jakim się zetknąłem był FORTRAN. W 3 klasie liceum w pamiętnym roku stanu wojennego. Nie było jeszcze pecetów więc programy były uruchamiane wzrokiem przez nauczyciela który wcielał się w rolę kompilatora/translatora 🙂 Dziś ze zgrozą trzeba stwierdzić że programowanie to jakaś elitarna dziedzina nawet wśród informatyków a informatyka w szkole to jakaś karykatura. Zresztą z matematyką jest podobnie. Ale nie ma co narzekać tylko po prostu trzeba rozwiązywać ciekawe zadania 🙂
Święte słowa. Trening umysłu jest bardzo potrzebny.
Z tego miejsca podziekuję panu Markowi za ten blog i trzymanie naszych umysłów w dobrej kondycji 🙂