Do oporu

6 sierpnia 2013
Marek Penszko

Zwykle na początku miesiąca proponowałem jakieś zadanie z konkursu zamieszczonego w Świecie Nauki w poprzednim miesiącu. Ponieważ jednak od niedawna artykuł z zadaniami konkursowymi dostępny jest wcześniej na stronie internetowej pisma, więc postanowiłem nieco zmienić zwyczaj. Odtąd będę nawiązywał do konkursu, proponując nie jedno z objętych nim zadań, lecz inne, ale takiego samego lub podobnego rodzaju.

W lipcu w Świecie Nauki gościły macki (jako Światowidy), czyli łamigłówki, które pojawiały się także w Łamiblogu. Odmian tego zadania jest przynajmniej kilka. Oto jeszcze jedna – dotychczas nie sadzona w moich ogródkach wyrafinowana odmiana z japońskich upraw.

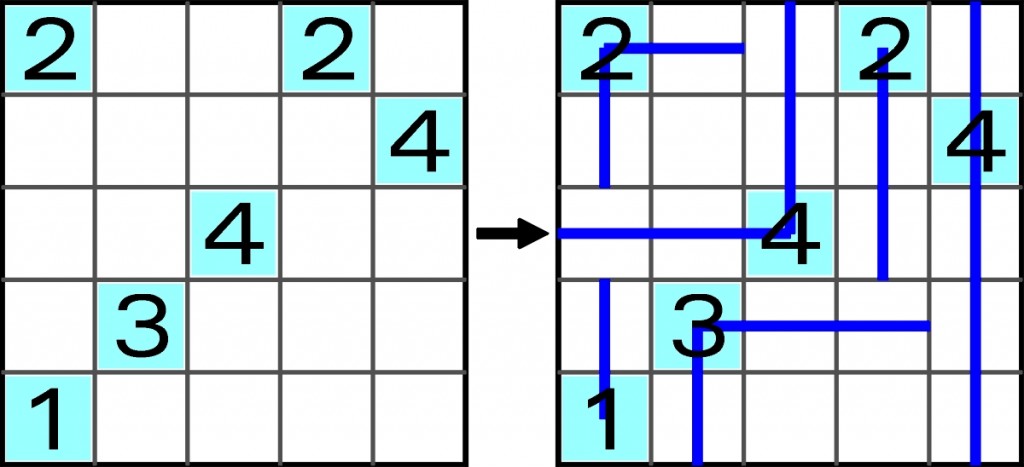
Liczby wysuwają macki w rzędach i kolumnach. W sumie każda powinna sięgnąć mackami tylu pól, jaka jest jej wartość. Specyficzne jest to, że każda macka musi sięgać „do oporu”, czyli do brzegu diagramu, granicy pola z cyfrą lub do granicy pola, którego sięga inna macka. Jednak dwie macki nigdzie nie mogą się zetknąć – nawet końcami na granicy pól.
Przykład:

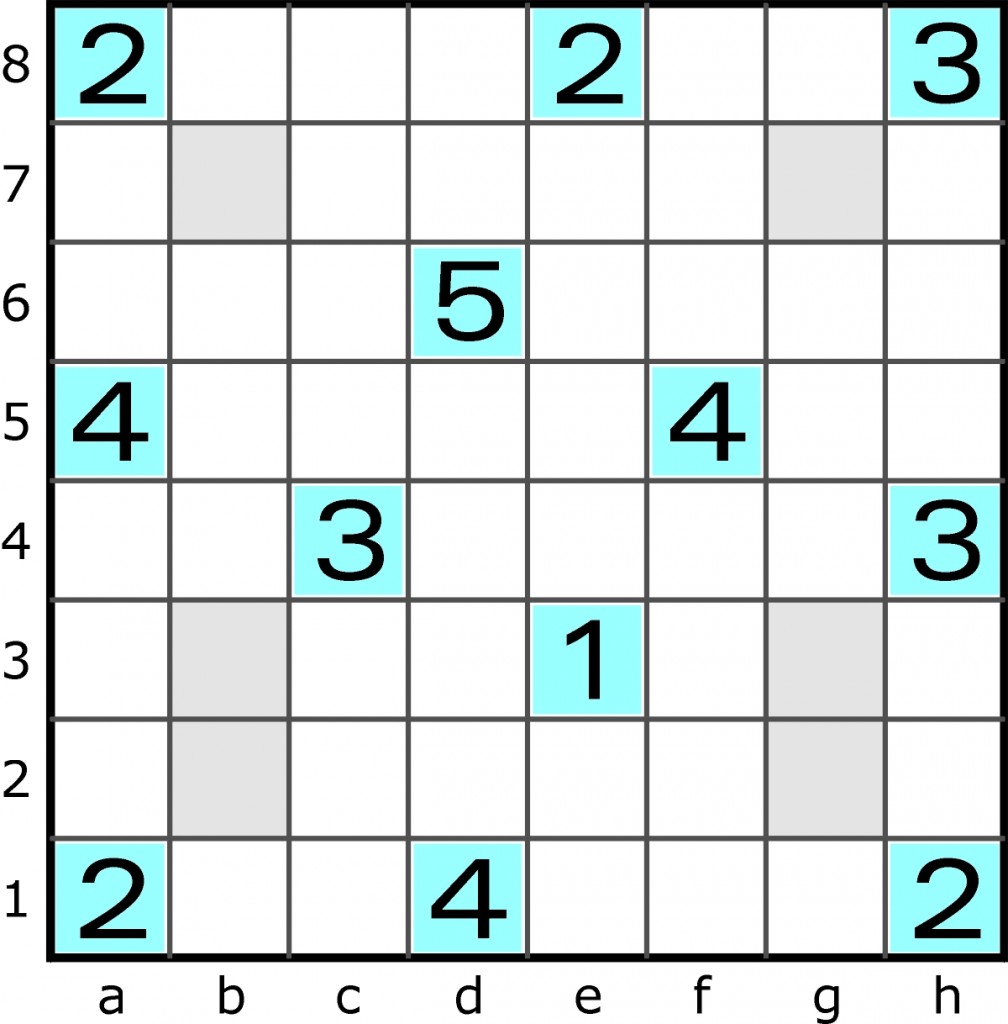
Suma cyfr jest mniejsza niż liczba pustych pól, więc wszystkich pól macki nie sięgają. W poniższym zadaniu już na starcie wiadomo, że sześciu szarych pól (b237, g237) macki na pewno nie sięgną. Ale poza nimi nie sięgną jeszcze jedenastu innych. Których?

Autorem pomysłu i zadania jest japoński puzzlemaster Inaba Naoki.

PS Dodatkowe zadanie dla ambitnych i cierpiących na nadmiar wolnego czasu. Przykład przed zadaniem ma więcej niż jedno podane rozwiązanie (ile?). Należy dokonać w przykładzie jak najmniej zmian tak, aby rozwiązanie było jedno. Zmianą jest wyłącznie przesunięcie cyfry na inne pole.