Zamiast dwu potęg
Około roku 1770 po dłuższej „zabawie” liczbami matematyk angielski Edward Waring doszedł do wniosku, że każdą liczbę naturalną można przedstawić jako sumę co najwyżej 4 kwadratów lub 9 sześcianów, lub 19 czwartych potęg, lub 37 piątych potęg, lub 73 szóstych itd. W tym samym roku matematyk francuski Joseph Lagrange dowiódł słuszności hipotezy dla kwadratów. Na dowody dla wyższych potęg trzeba było czekać do XX wieku, a z najtrudniejszym do dowiedzenia podwójnym kwadratem (n^4) dopiero w roku 1986 ostatecznie rozprawił się Ramachandran Balasubramanian.
2013 z dwu kwadratów się nie złoży, za to z trzech aż na cztery sposoby, w tym jeden osobliwy, bo podstawy dwu kwadratów są w nim połówkami roku, który nam nastał:
38^2 + 20^2 + 13^2 = 2013
Jeśli chodzi o sześciany, to na obecny rok nie wystarczą dwa, ani trzy, ani nawet cztery. Potrzeba pięciu, w tym jednej powtórki:
12^3 + 5^3 + 5^3 + 3^3 + 2^3 = 2013
Teraz miała być zagadka raczej komputerowa i trochę podstępna, ale nie wyszła. Zamierzałem zachęcić programistów do szukania zapisu 2013 w postaci sumy dwu dowolnych potęg liczb całkowitych. Podstęp miał polegać na tym, że podstawą mniejszej potęgi nieparzystej powinna być, jak sądziłem, liczba ujemna (z potęgami dodatnimi na zapis nie ma szans), więc suma w gruncie rzeczy okazałaby się różnicą. Gwoli jasności przykład takiego zapisu dla roku, który dopiero nastanie:
45^2 + (-2)^3 = 2017
Niestety, poniewczasie okazało się, że dla bieżącego roku sztuczka z nieparzystą potęgą się nie uda, czyli równanie
x^n + y^m = 2013
nie ma rozwiązań w liczbach całkowitych, uwzględniając także ujemne y.
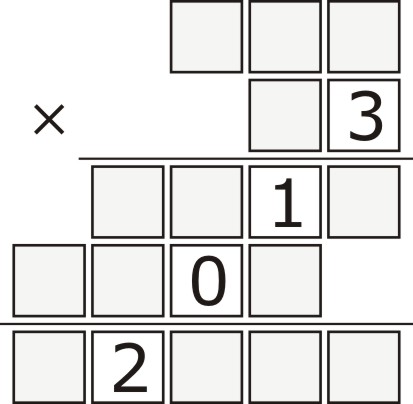
Zagadka z 2013 jest więc całkiem inna i prostsza, czyli dla wszystkich. Polega na rozszyfrowaniu mnożenia, w zapisie którego ujawniono cyfry tworzące obecny rok.
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co kilka dni.

Komentarze
638×83=52954
To zadanie ma 7 rozwiązań.
802*53;
803*53;
669*63;
835*63;
836*63;
568*93;
668*93.
Trochę przydużo.
Do: Antyp
Wyglada na to, ze rozwiazales troche inne zadanie.
a
638*83
Pozdrawiam 🙂
Faktycznie „udało” mi się rozwiązać ciut inne zadanie.
Prawidłowe rozwiązanie 638*83
Odp: 638*83 = 52954.
Przypuszczam, że rozwiązań może być więcej niż jedno, dlatego jeszcze postaram się znaleźć albo kolejne rozwiązania albo dowód, że rozwiązanie jest jedno.
Odnosząc się do długiego wstępu przed tym zadaniem chciałbym zauważyć, że bardzo mnie smuci fakt, że w dzisiejszych czasach najczęściej te rzeczywiście trudne problemy matematyczne, czekające na rozwiązanie wiążą się z bardzo skomplikowanymi obliczeniami komputerowymi. Słyszy się o komputerach, które w tempie niewyobrażalnym przeszukują miliony kombinacji, by znaleźć tę właściwą.
Ja nie jestem wielkim komputerowcem i mnie problem matematyczny bądź logiczny przyciąga właśnie wtedy gdy ja jestem w stanie się z nim zmierzyć bez udziału komputera, a jeszcze lepiej jest wtedy gdy komputer nie jest w stanie pomóc głowie. Takie łamigłówki mają dla mnie największą wartość.
Ale się rozgadałem…. no cóż
Dlatego samą głową dochodziłem do kolejnych wniosków:
1. Cyfra dziesiątek pierwszego czynnika to 3 (szybko wykluczyłem drugiego kandydata w postaci cyfry 7)
2. Cyfra dziesiątek drugiego czynnika to 8
3. Cyfra jedności pierwszego czynnika to też 8
4. Cyfra setek pierwszego czynnika to 6
A nasz iloczyn to oczywiście: 638 * 83 = 52954
P.S. Jedyne możliwe rozwiązanie. 🙂
Pozdrawiam
Chyba wszyscy matematycy niechętnym okiem patrzą na rozprawianie się z trudnymi problemami przy użyciu komputerów – uważają ten sposób za „prostacki”. Z drugiej strony programowanie nie zawsze sprowadza się do algorytmu siłowego, który sprawdza wszystkie możliwości – często także stanowi trudną, wciągającą łamigłówkę.
mp