Pento-sudoku
Układanie łamigłówki to także łamigłówka – często ciekawsza i trudniejsza niż rozwiązywanie onej po ułożeniu. Od paru dni główkuję nad skrzyżowaniem sudoku z pentominem. Ogólna koncepcja jest taka:
1) z wszystkich 12 figur pentomina
i jednego kwadratowego tetromina układamy kwadrat 8×8; komu pentominowe układanki są nieobce, ten wie, że taki kwadrat (z tetrominem w samym środku) można ułożyć na 65 różnych sposobów, np. tak:
2) w 64 pola należy wpisać cyfry od 1 do 8 tak, aby:
a) w każdym rzędzie i w każdej kolumnie było się osiem różnych cyfr;
b) w każdej figurze znalazły się różne kolejne cyfry (np. w jakimś pentominie 23456, a w tetrominie 5678).
W łamigłówce do rozwiązywania część cyfr byłaby oczywiście ujawniona – jak w sudoku.
Okazało się jednak, że warunek 2b należałby jakoś zmienić, ponieważ nie jest możliwe, aby przy zachowaniu poprzednich warunków w każdej figurze znalazły się różne kolejne cyfry. Dlaczego?
A dla tych, którzy wolą bardziej konkretne menu, proponuję podobną łamigłówkę, ale znacznie mniej sudokową.
Diagram należy podzielić na 12 różnych figur pentomina tak, aby suma cyfr objętych każdą figurą była równa 24. W rozwiązaniu wystarczy podać nazwy figur bez cyfry 5.
Zadanie pochodzi z ubiegłorocznych 24-godzinnych mistrzostw łamigłówkowych organizowanych co roku w Budapeszcie.
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co kilka dni.
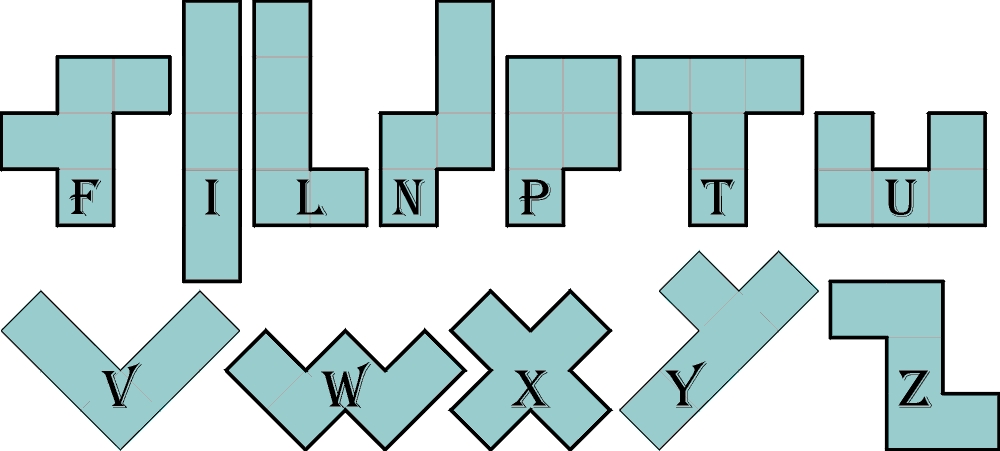



Komentarze
Ad. 2: LTUIFZ
Po kolei od góry kamienie bez 5
L T I U F Z
Wprawdzie niniejszy komentarz dotyczy poprzedniego wpisu „Co policzył Bazyli”, ale tam już chyba mało kto zajrzy, więc pozwoliłem sobie tutaj podać odpowiedź na pytanie „Ile jest różnych bezpiecznych ustawień największej liczby wieżoskoczków na szachownicy (n×n)?”
Napisałem program (http://ideone.com/6bKsz) i wyszło mi:
1,1,1,3,6,21,75,415,2621
Dla planszy 10×10 i większych nie mam wyniku, bo program (oparty na naiwnym algorytmie sprawdzania wszystkich możliwości) jest mało efektywny i nie doczekałem wyniku.
Moim (skromnym) zdaniem program, a więc także i wyniki, są OK. Gdyby jednak – gwoli formalności – ktoś z doświadczonych programistów (C++) zechciał to potwierdzić – byłbym wdzięczny.
mp
Jak to w takich zadaniach bywa, końcówkę „widać” ze względu na ubogą różnorodność klocków
http://i.imgur.com/B8JTX.jpg
Karzymie, co oznaczają żółte kreski? Zapewne wiąże się to z „końcówką, którą widać”, ale nie mogę skojarzyć, o co chodzi.
mp
Udało się posortować ustawienia wygenerowane w arkuszu 🙂
Również otrzymałem 75 różnych ułożeń dla n=7 i 415 różnych ułożeń dla n=8. Poniżej listy ustawień wieżoskoczków:
n=7 http://wklej.org/hash/06f9bbd6658/
n=8 http://wklej.org/hash/89f2c7196aa/
Dzięki. Wszystko jak na dłoni. Skopiowałem, ale literki usunąłem – zapis pozycji jest jasny bez nich.
mp
Pojęcie sąsiedztwa występujące w punkcie 2b możemy rozszerzyć na sąsiedztwo „okrągłego stołu”. I w ten sposób sąsiadami byłyby nie tylko np. 23456, ale i np. taki zestaw cyfr 78123.
Być może teraz, po modyfikacji punktu 2b, uda się powiązać sudoku z pentominem.
Andrzeju, nasze myśli – nie po raz pierwszy zresztą – podążają podobnym torem. Taką właśnie modyfikację wcieliłem w życie i zadanie jest już gotowe (nie było lekko) – pojawi się prawdopodobnie w ŚN za jakiś czas.
mp
@Witman: z braku czasu nie bawiłem sie dalej, ale spróbuj mojego algorytmu napisanego w ansi C ( wtym jezyku programuje na codzien firmware’y):
http://ideone.com/motBhU
Ewentualnie zrob dynamiczną listę ListElement, żeby dała radę pomieścić unikalne wyniki.
Algorytm daje te same liczby unikalnych układów.
W linku N jest ustawione na 6, ale nic nie stoi na przeszkodzie zwiększyc je do dowolnej liczby (tylko uważać trzeba na wielkość tablicy ListElement, lub zrobic listę dynamiczną).
Mam nadzieje, ze to pomoże w dalszych badaniach.
Pod tym linkiem:
http://ideone.com/7TMwS7
zmodyfikowany lekko kod wypisujący wszystkie unikalne układy, w tym przypadku dla N=7
Żółte kreski nic nie znaczą, gdy zadanie już jest rozwiązane. W trakcie rozwiązania rysuję sobie która liczba musi być połączona z którą. Dzięki temu nie muszę rysować całej figury od razu.
Szczerze podziwiam osoby, które potrafią wyrysowywać tego typu zadania bez takiego częściowego wspomagania się.
Zoptymalizowałem mocno swój program (http://ideone.com/qkWf8W) i uruchomiłem na nowym klastrze spoja Cube(http://pl.spoj.pl/clusters/). Dzięki temu wydłużyłem ciąg o kolejne dwie wartości:
1,1,1,3,6,21,75,415,2621,21066,195485…
Niestety na więcej nie bardzo można liczyć. Złożoność zastosowanego algorytmu (O(n!^2)) jest bardzo „nieprzyjemna” i szybkość współczesnych komputerów na wiele się nie zdaje.
Dla zainteresowanych podam, że dla n=9 wynik uzyskałem w 0.6s, dla n=10 w ok. 40s, a dla n=11 – w ponad godzinę.
Tym samym na wynik dla n=12 trzeba byłoby czekać około 4 dni, dla n=13 – ponad rok, a dla n=14 – … ponad 100 lat!
A może da się wyznaczyć wartości ciągu bez sprawdzania wszystkich możliwych ustawień…?
@Wiąz
Ładny, krótki program. Gratulacje.
Aby spełnić warunek 2b (bez modyfikacji zproponowanej przez Andrzeja), w każdej figurze pentomina musiałyby się znaleźć cyfry 4 i 5 (plus jedna z nich w wenętrznym kwadracie). Byłoby ich więc zdecydowanie za dużo.
Pento-sudoku nie mozna ulozyc, bo w kazdej figurze byloby 4 i 5, czyli w sumie tych cyfr byloby za duzo (moze byc tylko jedno 4 i 5 w kazdym rzedzie).
Figury bez 5: F, I, L, T, U, Z.
a
Jest taki lemat z teorii grup, nazywa się lemat Burnside’a. Czasem bardzo przydaje się przy zliczaniu w różnych zadaniach matematyczno-logicznych 🙂 Wychodzi z niego dla n=8: (2766 + 2 * 4 + 94 + 2 * 0 + 2 * 226) / 8 = 415. Tak czy inaczej te liczby punktów stałych dla poszczególnych przekształceń też mi program znalazł, ale może dałoby się to zrobić nawet na piechotę 😉
@Karwer dzięki, byłem pewny, że próbuję wynaleźć jeszcze raz koło ;)… jednak bardzo daleki byłem od tego… Próbuje teraz rozgryźć Twoje równanie 🙂 … takie łamigłówki potrafią mnie nieźle wciągnąć… coś chyba jakiś niespełniony matematyk odzywa się we mnie 🙂
Figury bez cyfry 5:
L T I U Z F.
Karwerze, Wiązie i inni rozwiązywacze zagadki lematu Burnside’a:
byłoby miło, gdyby ktoś z Was podrzucił link do strony, na której ten temat jest w miarę przystępnie wyjaśniony (nie koniecznie po polsku, ale – jeśli to możliwe – bez kobylastych równań).
mp
PS jeśli oczywiście zrozumienie przystępnego wyjaśnienia przez niematematyka jest w ogóle możliwe bez konieczności przestudiowania paru opasłych ksiąg.
1) W każdej figurze wystąpi 4 i 5. (12345,23456,34567 albo 45678).
2) 5 nie występuje w L, I, Z, U, T, F
Na razie tylko guglując znalazłem kilka forów z przykładami, głównie kolorowaniem różnych figur i brył… ale chyba nic ciekawego, czego by na pierwszej lub drugiej stronie wyników gugla Pan nie znalazł, więc nie śmiecę linkami 🙂 Na razie próbuje pozbierać do kupy grupy przekształceń, bo niektóre symetrie można osiągnąć kombinacją dwóch innych symetrii… a to się chyba wyklucza… krótko mówiąc, jest ciężko 🙂 po pracy wniknę głębiej w temat… 🙂 będę także szukał czegoś dla ‚niematematyków’ raczej :):)
Na dole strony jest przystępne wyjasnienie jesli chodzi o symetrie kwadratu i daje jako takie pojęcie o punktach stałych… ale mimo to nie potrafię tego powiązać z równaniem Karwera (przynajmniej nie teraz i nie w pracy 🙂 )
http://www.jaapsch.net/puzzles/theory.htm
Z lematem Burnside’a zetknąłem się niedawno rozwiązując nowe zadanie na polskim spoju (http://pl.spoj.pl/problems/AL_01_05). Zadanie wprawdzie rozwiązałem, ale lematu w pełni nie ogarnąłem :(.
W sieci znalazłem dość przystępny artykuł (po angielsku, mało wzorów + rysunki) na temat kolorowania szachownicy (http://www.rose-hulman.edu/mathjournal/archives/2008/vol9-n2/paper8/v9n2-8pd.pdf).
Jeśli tylko znajdę czas, spróbuję wykorzystać to w moim programie dotyczącym wieżoskoczków. Powinno dać się wtedy wyznaczyć kilka następnych wyrazów ciągu, bo odpadnie konieczność sprawdzania, czy kolejne znalezione ustawienie jest równe (z dokładnością do obrotu i symetrii) któremuś z już wyznaczonych.
Niestety rekurencyjne wyznaczanie wszystkich bezpiecznych ustawień decyduje o czasie działania programu, więc zamiast algorytmu o złożoności O(n!^2) dostaniemy O(n!). Na znaczne wydłużenie ciągu i tak nie można więc liczyć.
PS
Gdyby Karwer był tak uprzejmy ( 🙂 ) i wyjaśnił skąd się wzięły takie a nie inne liczby w Jego wzorze, byłoby łatwiej.
Niech g0 oznacza identyczność, g1 obrót szachownicy o 90 st. w prawo, g2 o 180 st., g3 o 270 st., a h symetrię osiową względem osi pionowej. Mamy (2766 + 4 + 94 + 4 + 0 + 226 + 0 + 226) / 8, gdzie kolejne składniki sumy to liczby punktów stałych (poprawnych ustawień wieżoskoczków, których nie zmienia dane przekształcenie) odpowiednio przekształceń g0, g1, g2, g3, hg0, hg1, hg2, hg3. Jak to nie pomoże, to podeślę jakieś linki 🙂
Załapałem o co chodzi w lemacie Burnside’a i wykorzystałem go w programie.
Teraz, po znalezieniu kolejnego ustawienia wieżoskoczków, sprawdzam czy taki układ jest punktem stałym dla każdego z ośmiu możliwych przekształceń kwadratu (identyczność, 3 obroty: 90, 180 i 270 stopni i 4 symetrie). Właściwie, to sprawdzam tylko 5 przekształceń (bez identyczności, bo tam każdy układ jest punktem stałym i bez symetrii w poziomie i w pionie, bo takie symetryczne układy wieżoskoczków dopuszczalne są tylko dla n=1).
Niestety, jak pisałem wcześniej, ta optymalizacja pomogła tylko trochę. Teraz, dało się wyznaczyć 11 wyrazów ciągu (http://ideone.com/QWop6c) w nieco ponad 0,5s (wcześniej, 9 wyrazów w ok. 1s). Dodatkowo, wyznaczyłem jeszcze trzy wartości (dla n=14 zajęło to 9 minut), więc ciąg wygląda teraz następująco:
1,1,1,3,6,21,75,415,2621,21066,195485,2083543,24744474,323438322…
W końcu zalapalem punkty stale:) jak widać najwięcej powtarzających się układów jest przy obrotach o 180 st.
Co prawda to nie na to forum, ale jadąc dzis do pracy zastanawiałem sie, czy istnieje taka geometria gdzie korzystając z lematu dostaniemy wartość ułammkową…
Dwie godziny później… 🙂
1,1,1,3,6,21,75,415,2621,21066,195485,2083543,24744474,323438322,4596672672…
Czy OEIS zostało uaktualnione? 🙂
Rozumiem, że chodzi o uzupełnienie OEIS ciągiem Witmana:
Number of inequivalent (essentially different) ways of placing n nonattacking empresses on n X n board,
czyli wariant ciągu A137774
Decyzja należy oczywiście do autora ciągu.
mp
Oczywiście to miałem na myśli. Podwoje OEIS czekają na Witmana:) byłeś pierwszy! Brawo!
P.S.
Na koniec tylko link do mojej wersji programu: http://ideone.com/sCtgXg
A gdyby warunek 2b żądał tej samej sumy cyfr – trzeba by się zastanowić czy w środkowym kwadracie miałoby być tyle samo co dla pentomin czy mniej, a może więcej?
Nie da się wypełnić cyframi pento-sudoku w taki sposób, aby sumy w każdym pentominie i kwadracie były takie same.
Sprawdziłem że gdyby dopuścić iż kwadrat ma inną sumę (mnieszą lub większą) niż pentomino to nie można uzyskać tych 12 jednakowych sum dla pentomin. W najlepszych układach jest ich tylko 6. Więc warunek typu suma odpada. Ale możnaby sprawdzić taki: pięciu cyfrom każdego kamienia pentomina przyporządkowujemy 3 plusy i 2 minusy i jeśli uda się uzyskać określoną wartość dla każdego kamienia to zaliczamy układ. dla kwadratu 2 plusy i 2 minusy i być może inna wartość niż dla pentomin.