Co policzył Bazyli

14 października 2012
Marek Penszko

Przypominam problem postawiony przez Esteona:
Ile jest różnych bezpiecznych ustawień największej liczby wieżoskoczków na szachownicy (8×8)?
Wieżoskoczek jest tzw. figurą „bajkową”, która porusza się jak wieża i skoczek. Ustawienia są:
– bezpieczne, jeśli żaden wieżoskoczek nie atakuje żadnego innego;
– różne, jeśli żadnego z nich nie można przekształcić w inne w wyniku obrotów lub/i odbić lustrzanych.

Odpowiedź na powyższe pytanie nie jest znana, co nasuwa podejrzenia, że problem jest trudny obliczeniowo. Brytyjski szachista Thomas Dawson znalazł „na piechotę” rozwiązania dla plansz do 6 × 6 włącznie i opublikował je w 1931 r. Oczywistym jest, że na planszy n × n da się ustawić co najwyżej n wieżoskoczków (n = 1, 2, 3,…). Ciąg liczb tych ustawień zaczyna się tak:
1, 1, 1, 3, 6, 21,…
Dalej, czyli dla n>6, jest mgła, której dotąd nikomu nie udało się rozwiać.
Tymczasem Bazyli w komentarzu podał rozwiązanie problemu Esteona znalezione przy wykorzystaniu arkusza kalkulacyjnego. W pierwszej chwili nie chciało mi się w to wierzyć – i słusznie. Wynik podany przez Bazylego jest bowiem liczbą wszystkich ustawień, a nie różnych. Ta liczba (2766) jest znana; znany jest także ciąg liczb wszystkich ustawień dla plansz różnej wielkości: 1, 2, 2, 8, 20, 94, 438, 2766, 19480, 163058 ,… (OEIS A000903). Schody zaczynają się przy próbie przekształcenia wszystkiego w różne. Dotąd nikt tych schodów nie pokonał dla n>6. Z lenistwa?

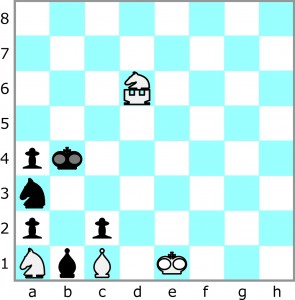
Na zakończenie wieżoskoczkowego tematu zwykła dwuchodówka, ale oczywiście z jedną niezwykłą figurą.

Wystarczy wskazać pierwszy ruch białych.
Zadanie liczy sobie 123 lata, ale przez ten czas wcale nie „zmiękło”. Wciąż jest twardym orzechem.

Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co kilka dni.