Jednym zdaniem
Dawno nie było w Łamiblogu indugadki, czyli zagadki (a właściwie łamigłówki) indukcyjnej. Pora nadrobić zaległości.
Przypominam, w czym rzecz: mamy przykład zadania, czyli diagram w większości pusty, i jego rozwiązanie, czyli diagram wypełniony i… nic poza tym. Inaczej mówiąc, brak jest instrukcji, więc trzeba samemu wywnioskować (wyindukować) – na podstawie rozwiązania przykładu – jakie są reguły zadania, które określają sposób wypełniania diagramu. A po wywnioskowaniu rozwiązać inne zadanie, korzystając z tych domniemanych reguł.
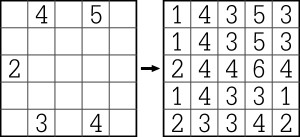
Przykład z rozwiązaniem wygląda tak:
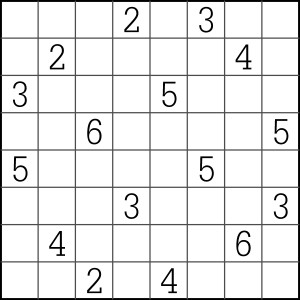
A zadanie tak:
Przypominam też, że lubię łamigłówki, których reguły są proste i krótkie, więc nie warto szukać zbytnich zawiłości, rządzących wpisywaniem cyfr w kratki. Reguły można ująć w jednym zdaniu niezbyt rozwiniętym.
Będę od razu uwalniał wszystkie komentarze z rozwiązaniem, zawierającym podane tylko cztery narożne cyfry (bez rozszyfrowanej zasady), a przy pierwszym poprawnym dopiszę, że jest OK.
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co kilka dni.

Komentarze
Na przemian, dodajemy i odejmujemy po kolei liczby wokół. W środek wpisujemy wynik bez znaku. Mam tylko nadzieję, że pogoda pozwoli posiedzieć w domu i pomyśleć nad zadaniem. Jak na razie… piękna majówka!!!
Uważam, że rozwiązań jest bardzo dużo. Regułę można zapisać też równoważną: w środku jest bezwzględny wynik różnicy sum liczb stykających się bokiem i tych stykających się rogiem. Jedno z rozwiązań:
11122311
12313145
31315414
14611115
51211534
41131413
14312161
31234112
Reguła – oczywiście – powinna być taka, aby rozwiązanie było tylko jedno.
mp
Teraz widzę, ze lewy dolny róg podpowiedzi wylamuje się moim regułom.
No, długi weekend pozwolił przysiąść na chwilkę i odnowić znajomości z dawno nie odwiedzanymi ( 🙁 ) stronami… 🙂
Cztery narożne cyfry począwszy od lewego górnego rogu zgodnie z ruchem wskazówek zegara:
0011
Pozdrawiam(y) 🙂
To jest OK!
mp
A oto i reguła:
Liczba w każdym okienku mówi, ile liczb nieparzystych ją otacza.
I pełne rozwiązanie:
00023320
22245542
33435653
55636575
55636575
33435653
44445564
11214331
Muszę przyznać, że na początku rozwiązywania strasznie mnie myliły pola, w których wpisywane były parzyste cyfry, bo narzucało mi się spontanicznie od razu myślenie, że ta cyfra mówi, ile PARZYSTYCH cyfr ją otacza, a nie nieparzystych. I rozwiązywanie podążało w błędnym kierunku. 🙂
Każda liczba mówi ile jest wokół niej liczb nieparzystych.
Zasada:
Każda liczba informuje, ilu ma nieparzystych sąsiadów.
Rozwiązałem, ale widzę, że uprzedziła mnie neon.ka 🙁
00023320
22245542
33435653
55636575
55636575
33435253
44445564
11214331
Zamiast jednego zdania jedna zwrotka:
Wartosc danej liczby
zawsze oznacza,
ile nieparzystych
liczb ja otacza
a
Zasada najkrócej – do każdej kratki wpisywana jest liczba nieparzystych sąsiadów (również ukośnych)
doszedłem do tego samego rozwiązania co neon.ka: 0011
zasada: każda cyfra diagramu przedstawia ilość cyfr nieparzystych będących z nią w bezpośrednim sąsiedztwie (również samym narożnikiem)
0 0 0 2 3 3 2 0
2 2 2 4 5 1 4 2
3 3 4 3 5 6 5 3
5 5 6 3 6 5 7 5
5 5 6 3 6 5 7 5
3 3 4 3 5 6 5 3
4 4 4 4 5 5 6 4
1 1 2 1 4 3 3 1
Własnie wziąłem sie w wolnej chwili za to zadanie… ale mimo udzielonych juz poprawnych odpowiedzi, jakoś nie moge wpaść na zasadę rządząca tym zadaniem… 🙁 nie mogę rozgryźć tego orzeszka 🙁 Czuje sie pobity! Zaćma jakaś, czy co? Kurcze, wydaje sie, że próbowałem juz wszystkiego :):):) kurcze…
Choc znalazłem jedną, mozna to nazwać regułą, dla każdego rzędu poziomego sumowanie i odejmowanie naprzemienne daje wynik 4, ale w pionie nie mogę nic znaleźć… 🙁