9 hetmańskich krów

15 marca 2012
Marek Penszko

Poprzednio wspomniałem o przesuwance Przeganianie krów, która była w zestawie zadań na ubiegłorocznych 20. Łamigłówkowych Mistrzostwach Świata w Egerze. Przypominała japońskie przesuwanki Satogaeri, ale bardziej skojarzyła mi się z szachami i pewnie dlatego zwróciłem na nią uwagę. Występujące w niej elementy (kółka) nazwane „krowami”, można by właściwie uznać za hetmany, a całość za wariację na temat najbardziej znanego zagadnienia matematyczno-szachowego – problemu 8 hetmanów. W uogólnionej formie problem polega na rozmieszczeniu n hetmanów na planszy n × n tak, aby figury się nie atakowały. Ściślej, chodzi o ustalenie, ile jest całkowicie różnych rozwiązań dla konkretnego n. Dziś uporanie się z tym problemem sprowadza się do napisania prostego programu, choć dla dużych n na efekt trzeba trochę czekać; w XIX wieku ponad 70-letni Gauss długo zmagał się z wariantem dla standardowej szachownicy (n = 8).

Wracając do przesuwanki z WPC, jej autor, Pál Madarassy, skorzystał z jednego z 46 podstawowych rozwiązań problemu dla n = 9, sprytnie przesuwając w nim każdego zmienionego w krowę hetmana o 4 pola w rzędzie lub kolumnie i – łamigłówka gotowa.
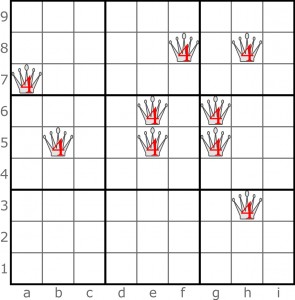
Dokładnie tak samo powstało poniższe zadanie, ale od tego z Mistrzostw jest trochę trudniejsze (brak pewniaka na początku):

Należy więc cofnąć ruchy, czyli przesunąć każdego hetmana o 4 pola poziomo lub pionowo (nie na ukos) tak, aby w każdym wierszu, kolumnie i w każdym sektorze 3 × 3 (nawiązanie do sudoku) znalazł się jeden hetman. W przeciwieństwie jednak do japońskich przesuwanek podczas wykonywania ruchów hetmany mogą przechodzić przez pola, na których stoją inne – tak, jakby pola te były puste – a także trasy ruchów mogą się przecinać. Ponadto jest jeden dodatkowy warunek, wykluczający dwa rozwiązania: hetmany nie mogą stać na sąsiednich polach, także stykających się tylko rogami. Ten warunek wynika bezpośrednio z powiązania łamigłówki z problemem 8 (9) hetmanów.

Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co kilka dni.