Garść forintów
Wracam do mamony i do ubiegłorocznych mistrzostw świata w Egerze.
Łamigłówka z banknotami zamieszczona we wpisie z 30 stycznia nie była jedyną pieniężną na tej imprezie. W zestawie zadań nie zabrakło także bilonu i to w bardziej rzeczywistej formie niż w przypadku papierowej waluty – nieco wirtualnej ze względu na nigdzie na świecie nie emitowane nominały 3 i 4.
Na ogół bilon, a ściślej tzw. drobne, czyli monety o wartościach mniejszych niż jednostka podstawowa, mają nominały takie, jak w przypadku złotego, euro czy dolara: 1, 2, 5, 10, 20, 50. Zdarzają się, i to nierzadko, odstępstwa od tego ciągu; pojawia się np. 1/2, ale częściej na skutek inflacji niektóre albo wszystkie drobniaki tracą siłę nabywczą i znikają, a ich rolę jakby przejmują jednostki podstawowe o identycznych nominałach (tak jest w przypadku forintów, filléry istnieją tylko w teorii).
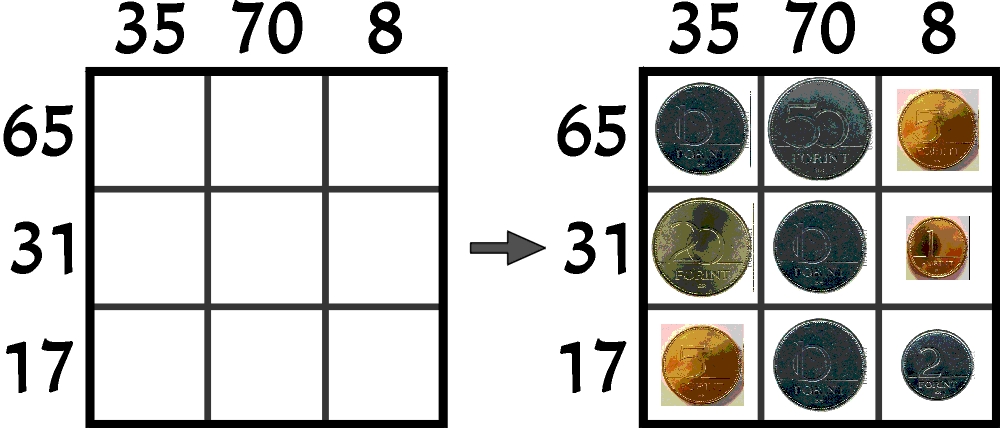
Pomysł węgierskiego zadania jest bardzo prosty. Rozmieszczamy n^2 monet we wszystkich kratkach diagramu n×n, wypisujemy przy brzegach sumy wartości monet w wierszach i kolumnach, potem usuwamy bilon i – łamigłówka gotowa. Chodzi oczywiście o odtworzenie rozmieszczenia monet na diagramie.
Przykład:
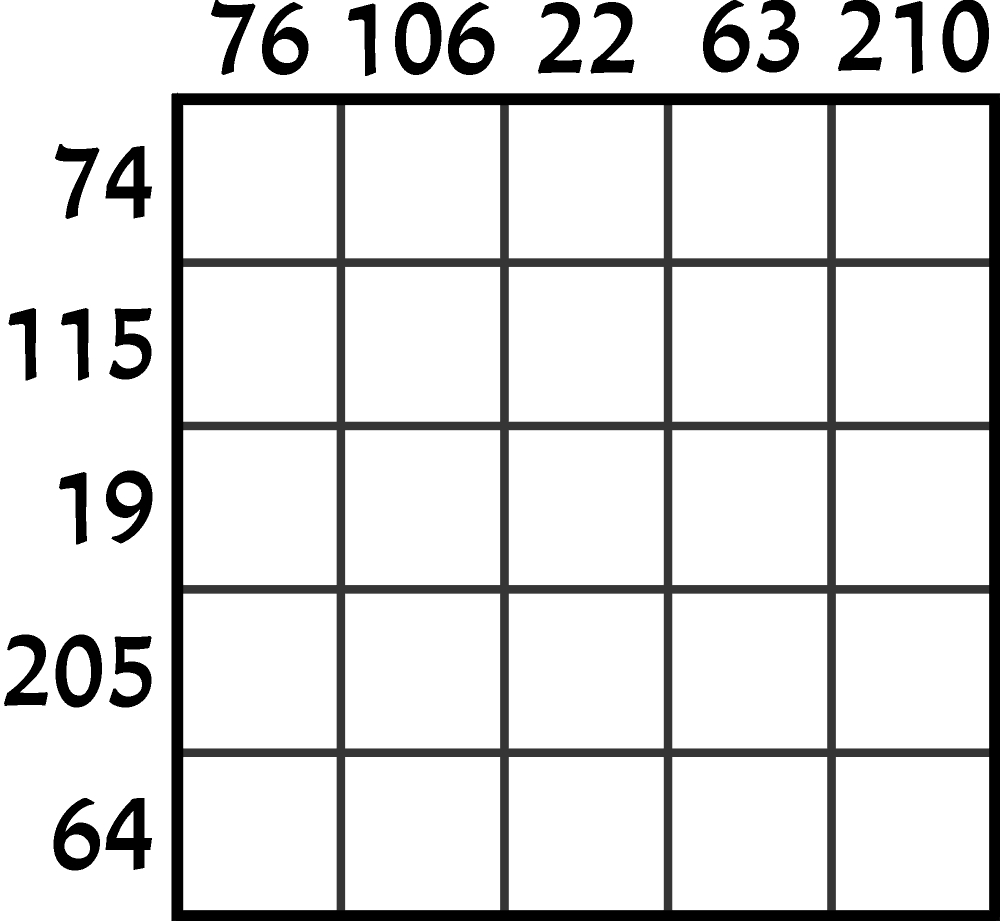
Możliwe wartości monet są znane (1, 2, 5, 10, 20, 50), ale ile razy występuje każda z nich – nie wiadomo. Czy w związku z tym podanie prawie wszystkich 2n sum, zakładając że są różne – jak w poniższym zadaniu z mistrzostw – jest zawsze konieczne?
Napisałem „prawie„, bo jedną sumę można oczywiście pominąć, ale czy może być ich mniej niż 2n – 1?
I drugie pytanie dodatkowe: czy wypisanie wszystkich sum zawsze jednoznacznie określa układ monet?
W rozwiązaniu wystarczy podać, w ilu miejscach sąsiadują ze sobą w rzędzie (nie na ukos) dwie monety, których suma jest liczbą pierwszą.
Monety można uznać za „uboższą” odmianę popularnego przed sześciu laty zadania. Jakiego?
A jeśli umówimy się na forinty, to łamigłówka będzie dziś nie mniej wirtualna niż wspomniane na początku zadanie z banknotami, bo monet o wartościach 1 i 2 nie ma w obiegu na Węgrzech od czterech lat.
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.

Komentarze
Miejsc takich jest dokładnie 4 🙂
Pamiętam, nie wiem czy teraz, że nominał 3 był u naszych sąsiadów zza Buga:)
Rzeczywiście, do 1999 r. http://pl.wikipedia.org/wiki/Rubel_bia%C5%82oruski
Widocznie źle zrozumiałem co należy podać w odpowiedz, bo miejsca na pomyłkę nie ma. Jeżeli chodzi pytanie „w ilu miejscach sąsiadują ze sobą w rzędzie (nie na ukos) dwie monety, których suma jest liczbą pierwszą” zrozumiemy, że rzeczywiście ile w rzędzie jest takich miejsc to 4, a jeżeli w rzędzie i kolumnie to 5. No chyba, że jakieś liczby pierwsze przegapiłem…. ale wszystkie sumy się zgadzają, więc po prostu musi być dobrze 🙂
Początkowo sądziłem, że błąd polega na nie uwzględnieniu sumy 2 (zdarza się czasem zapomnieć, że jest ona liczbą pierwszą). Po wyjaśnieniach widzę, że chodzi o coś innego.
Przyjąłem zasadę – i we wpisie jest to zaznaczone – że rząd jest zarówno poziomy, jak i pionowy, natomiast jeśli jest poziomy to jest wierszem, a pionowy – kolumną. Taka terminologia jest zgodna z przyjętą w matematyce (proszę zerknąć do Wikipedii pod hasła „macierz” http://pl.wikipedia.org/wiki/Macierz i „kwadrat magiczny” http://pl.wikipedia.org/wiki/Kwadrat_magiczny_%28matematyka%29
mp
Może i bialoruski, ale ja pamiętam jeszcze ZSRR i tamte ruble:)
10,02,10,02,50
05,50,05,05,50
01,02,01,05,10
50,50,05,50,50
10,02,01,01,50
Poziomo (1,2), (2,1), (2,1), (1,1)
Pionowo (2,5)
Po chwili zastanowienia przyznaję 100% racji, pomyliłem wiersz z rzędem, a raczej rząd z wierszem.
Może choć trochę usprawiedliwi mnie fakt zamiłowania do książek o matematyce ze świata anglojęzycznego. A tam (proszę zajrzeć: http://en.wikipedia.org/wiki/Matrix_%28mathematics%29 ) mamy do czynienia z „row” i „column”. „Row” również jest rzędem w kinie i teatrze, stąd prosty wniosek czym jest rząd w Polsce.
Ale błąd mój jest większy. Wszak rząd macierzy to po angielsku „column rank”.
A więc nic innego mi nie pozostaje jak przyznać 200% racji.
Anglicy też czasem zamiast „row” piszą „line”. Ale generalnie za to „zamieszanie” odpowiedzialne jest wojsko – na musztrze (jak pamiętam) są rzędy (szeregi) i kolumny, a wierszy brak (są tylko wiersze wojskowe i… piosenki). W dodatku grupa złożona z szeregów i kolumn tworzy kolumnę, że już o piątej kolumnie nie wspomnę. Nic dziwnego, że w wojsku jest bałagan 🙂
mp
4 w wierszach + 1 w kolumnie = 5
a
Sum przy diagramie nie może być mniej niż 2n-1.
Brak dwóch sum w kolumnie (albo w wierszu) spowoduje możliwość zamiany rzędów.
Brak jednej sumy w kolumnie i jednej sumy w wierszu prowadzi do niemożliwości jednoznacznego wyznaczenia wartości monety na przecięciu tych rzędów.
Wypisanie wszystkich sum nie zawsze prowadzi do jednoznaczności rozwiązania.
Pewne układy monet (prostokątno-przekątniowe) tworzą wiele rozwiązań.
Liczba sąsiadów tworzących sumę liczby pierwszej: 5.
Nie wiem o jakie popularne sprzed sześciu lat zadanie chodzi, ale „Monety” skojarzyły mi się z „Mastermindem”.
Mi się skojarzyło z kakuro – jeśli popularne, bo niepopularnych podobnych było sporo, choćby survo (http://penszko.blog.polityka.pl/2009/09/16/same-sumy/ )
mp
A jakby tego było mało musimy jeszcze odróżnić rząd i nierząd. Twarde prawa logiki kazałyby przypuszczać, że ten drugi jest zaprzeczeniem tego pierwszego. Tymczasem logika ludzka tak bardzo różni się od tej matematycznej, że zdarza się iż z zamiłowania do nierządu ktoś trafia do rządu. A nierząd w sprawowaniu rządów (a nie: rzędów) zdecydowanie przeszkadza.
Oj, bałagan chyba nie tylko w wojsku jest 😉
Dziwne, komentarz z czwórką został ujawniony, co świadczy, że ta odpowiedź jest błędna.
A mi wychodzi dokładnie tak samo.
10,2,10,2,50
5,50,5,5,50
1,2,1,5,10
50,50,5,50,50
10,2,1,1,50
Wpisanie wszystkich nie zawsze jednoznacznie określa układ.
Przykład: kwadrat 2×2 i wszystkie sumy równe 3.
Pozdrawiam
Piotr
Pojęcie „rząd” obejmuje wiersze i kolumny
mp
[10, 2, 10, 2, 50]
[5, 50, 5, 5, 50],
[1, 2, 1, 5, 10]
[50, 50, 5, 50, 50]
[10, 2, 1, 1, 50]