Czterdzieści i cztery

24 stycznia 2012
Marek Penszko

Oparta na grze w okręty łamigłówka o takiej samej nazwie ma wiele odmian. Niektóre opisywałem; jest okazja, aby zaprezentować jeszcze jedną – będzie ona jakby wstępem do podobnego zadania, które przedstawię później.

Zacznę od przypomnienia podstawowego wariantu, bo może zajrzą tu nowicjusze.

Mamy akwen – kwadrat n × n kratek oraz flotę – okręty-prostokąty 1 × x kratek. Tradycyjnie, jak w grze, x określa liczbę masztów, czyli okręty 1 × 1 to jednomasztowce, 1 × 2 – dwumasztowce itd. (często zamiast żaglowców pojawiają się nazwy współczesnych jednostek – łodzie podwodne, pancerniki, niszczyciele itp.). Flota złożona z ustalonej, znanej liczby jednostek znajduje się na akwenie – okręty są dokładnie wpasowane w rzędy kratek, jednak ich położenie jest utajnione i zaszyfrowane liczbami przy brzegu diagramu.
Każda liczba oznacza, ile pól zajętych jest przez okręty w rzędzie (wierszu lub kolumnie), przy którym dana liczba jest umieszczona. Ponadto wiadomo, że żadne dwa okręty nie zajmują sąsiednich kratek, także stykających się tylko rogami. Zadanie polega na ustaleniu położenia wszystkich okrętów. Aby nie było dwuznaczności oraz by było ciekawiej i bardziej logicznie, często ujawniane są fragmenty jednostek (dziób, rufa, śródokręcie) lub wodne pola (linie faliste), których na pewno nie zajmuje żaden okręt.
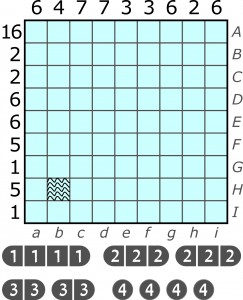
Oto mały przykład z rozwiązaniem:

Mam nadzieję, że dla nowicjuszy – kandydatów na wilków morskich – wszystko jest jasne.

Zanim przedstawię wspomnianą odmianę, proponuję spojrzeć na okręty nieco inaczej. Każdy maszt to jedna kratka, zaś gdyby we wszystkie okrętowe kratki wstawić jedynki, to liczby przy brzegu byłyby sumami tych jedynek. I właśnie w anonsowanej odmianie liczby są sumami, ale nie wyłącznie jedynek, bowiem w okrętowych kratkach pojawiają się różne cyfry, w zależności od rodzaju okrętu. Kratka-maszt jednomasztowca równa jest 4, dwumasztowca – 3, trójmasztowca – 2, czteromasztowca – 1.
Odmiana nosi nazwę „okręty ważone”.

Kolej na zadanie, które pochodzi z 12 Łamigłówkowych Mistrzostw Świata (Arnhem, 2003).

W rozwiązaniu wystarczy podać położenie czterech jednomasztowców, korzystając ze współrzędnych literowych przy brzegach.

A skąd „mickiewiczowski” tytuł – łatwo zgadnąć.

Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.