Heksagramagia
8 stycznia wspomniałem o wydanej pod koniec ubiegłego roku przez Wydawnictwo Literackie książce Iana Stewarta Gabinet matematycznych zagadek. Niebawem zadebiutuje na rynku kolejne dziełko tego autora – Jak pokroić tort i inne zagadki matematyczne, tym razem w wydawnictwie Prószyński i S-ka. To jakby potwierdzenie mojej teorii, że profesor z Warwick rozpisał się niczym nasz Józef Ignacy. Czy ilość idzie w parze z jakością? Można mieć drobne wątpliwości.
Zajrzyjmy do Gabinetu…. Jest w nim artykulik o gwiazdach magicznych uzupełniony takim oto zadaniem:
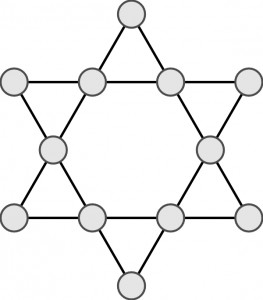
Wpisz liczby od 1 do 12 w pola, tak aby powstała gwiazda magiczna.
Czyli tak, aby każda linia złożona z czterech pól dawała tę samą sumę. (Podpowiedź: suma ta wynosi 26). A żeby łamigłówka była trudniejsza, poproszę, aby sześć liczb na końcach ramion też dawało po zsumowaniu 26.
Jak rozmieścić liczby?
To jest zadanie w stylu Dudeneya, czyli „znęcanie się” nad czytelnikiem, ewentualnie żart. Skojarzyło mi się z sudoku, w którym diagram byłby całkiem pusty, a instrukcja brzmiałaby:
wpisz cyfry od 1 do 9 w kratki tak, aby w każdym rzędzie i w każdej kolumnie występowały różne cyfry. A żeby łamigłówka była trudniejsza, poproszę, aby w sektorach 3×3 także występowały różne cyfry.
Oczywiście trochę przeginam, ale ogólny sens jest podobny – jedno i drugie to mordęga albo zabawa dla programisty.
Jednak to nie wszystko, bo gwóźdź programu tkwi w komentarzu do zamieszczonego w książce rozwiązania, które wygląda tak:
I byłoby OK, gdyby nie ów komentarz: to jedyne rozwiązanie (oczywiście z dokładnością do odbić i obrotów). Jak z tego wynika, pan profesor nie uważał na lekcji, bo całkiem różnych rozwiązań jest sześć. Jedno z pięciu pozostałych stanowi rozwiązanie poniższego zadania.
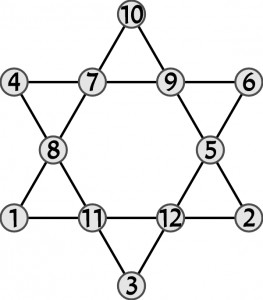
Instrukcja brzmi tak samo jak wyżej u Stewarta, ale trzy cyfry są już na właściwych miejscach – i dzięki temu łamigłówka jest łamigłówką.
Jaka liczba wskoczy w górne kółko?
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.


Komentarze
W górnym kółku znajduje się 2 🙂
W górnym jest 2.
Rzędami:
2
7,6,12,1
10,9
8,4,11,3
5
Na szczycie gwiazdy magicznej znajdzie się pierwsza liczba pierwsza.
Ocena niedostateczna 🙂 , czyli dwoja
a
Witam,
Zadanie o podanej przez Pana treści ma 2 różne rozwiązania. W górne kółko wchodzi liczba 2 lub 3. Rozwiązania te, zapisane w kolejności podania kółek w wierszach, od góry do dołu, to:
3, 7, 11, 2, 6, 4, 9, 8, 5, 1, 12, 10 oraz
2, 7, 6, 12, 1, 10, 9, 8, 4, 11, 3, 5.
Ciekawe w nich jest to, że drugie można uzyskać z pierwszego przez obrót o 60 stopni oraz zamianę ciągu 1..12 na 12..1.
Pozdrawiam
JW
Pierwsze rozwiązanie nie pasuje – nie spełnia warunku:
„A żeby łamigłówka była trudniejsza, poproszę, aby sześć liczb na końcach ramion też dawało po zsumowaniu 26”.
mp
W górnym tj. najwyższym kółku powinna się znaleźć dwójka 2 🙂
Rozwiązanie
2 7 6 12 1 10 9 8 4 11 3 5
Gdyby nie było warunku o sumie magicznej na końcach ramion gwiazdy, byłoby jeszcze inne rozwiązanie
3 7 11 2 6 4 9 8 5 1 12 10