Duży ptaszek

11 stycznia 2012
Marek Penszko

Ile najwięcej wielokątów można wyciąć z płaszczyzny – lub lepiej, by były granice, z koła – n>2 prostymi (cięciwami)? Niezbyt trudno ustalić, że n^2/2 – 3n/2 + 1. Tak jest, gdy każde dwie cięciwy mają punkt wspólny, a żadne trzy nie.
Wśród tych wielokątów będzie co najwyżej n(n – 2)/3 trójkątów, uwzględniając oczywiście część całkowitą wyniku.
Przykład:

Cięciw jest 7, wielokątów 15 (kropki), trójkątów 11 (czerwone kropki).

A teraz drugie pytanie, bardzo podobne: ile najwięcej wielokątów można wyciąć z koła n>2 cięciwami przy założeniu, że każdy z nich będzie trójkątem?
Może się to wydać dziwne, ale nie wiadomo, tzn. nie jest znany ogólny wzór, a konkretne efekty są pewne tylko dla małej liczby cięciw. Pewne jest także to, że trójkątów nigdy nie jest więcej, a z reguły mniej, niż wówczas, gdy inne wielokąty nie są wykluczone – np. dla 7 cięciw jest ich 10.

Proponuję mały „eksperyment ornitologiczny” z 6 cięciwami, zwłaszcza że tylko dla takiej liczby cięciw uda się wyciąć co najwyżej 7 trójkątów w obu przypadkach – czyli tyle samo niezależnie od tego, czy trójkątom będą towarzyszyć inne wielokąty, czy nie.

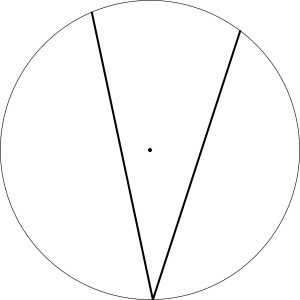
Dwie cięciwy wyprowadzone z jednego punktu na okręgu przypominają dużego ptaszka (v). Kąt między nimi równy jest 30 stopni.

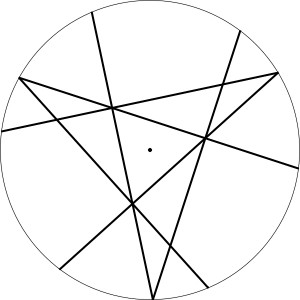
Ptaszka obrócono o 120 i 240 stopni wokół środka okręgu, a efekty obrotów nałożono na oryginał – i okazało się, że trzy ptaszki idealnie wycięły z okręgu siedem trójkątów:

Czy ktoś z Państwa potrafi wyprowadzić na tej podstawie wzory na długości skrzydeł ptaszka (cięciw) – dłuższego i krótszego – w zależności od promienia okręgu?

Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.