Kwadratowy ciąg

4 października 2011
Marek Penszko

Gdy przed rokiem zmarł Benoît Mandelbrot, twórca pojęcia „fraktal” i badacz obiektów określanych tym terminem, jeden z Łamiblogowiczów poinformował mnie o tym, sugerując, bym wspomniał na blogu o francuskim matematyku urodzonym w Warszawie. Wprawdzie fraktale są w jakimś sensie zagadkowe, ale żadna konkretna łamigłówka, która dopełniałaby wspomnienie, nie przyszła mi wówczas do głowy. Dopiero poniewczasie zauważyłem, że zadanie, które znalazło się w poprzednim wpisie, pasowałoby idealnie, bo  występuje w nim ciąg zwany czasem fraktalnym.

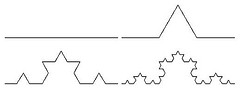
Najbardziej widoczną i widowiskową cechą fraktalu – w popularnym ujęciu – jest to, że każdy jego nieskończenie mały fragment okazuje się po powiększeniu kopią większego fragmentu. Ilustruje to np. proces tworzenia krzywej Kocha, przedstawiony poniżej (trzy początkowe etapy).

Co to ma wspólnego z ciągiem piśnięć Kurczaka Małego z wpisu poprzedniego?
PI, PIIP, PIIPIPPI, PIIPIPPIIPPIPIIP,…

Najpierw przywróćmy ciągowi formę matematyczną, czyli binarną, zastępując litery P zerami, a litery I jedynkami:
01, 0110, 01101001, 0110100110010110,…
A teraz „powiększamy” (lupa lub luneta) pierwszy wyraz i zauważamy (proszę uruchomić wyobraźnię), że w istocie zero jest parą 01, a jedynka parą 10 – tak powstaje drugi wyraz. Następnie przybliżamy drugi wyraz i dostrzegamy to samo – zera zmieniają się w zero-jedynki, a jedynki w jedynko-zera i mamy trzeci wyraz. Najazd kamery na trzeci wyraz powoduje analogiczny efekt – pojawia się czwarty wyraz itd.
Można też inaczej. Oddalamy się od jakiegoś długiego, np. 1024-cyfrowego wyrazu i „tracimy z oczu” cyfry na miejscach parzystych (załóżmy, że są mniejsze). Co zobaczymy? Oczywiście poprzedni wyraz.
Jest jeszcze kilka innych, już niefraktalnych sposobów tworzenia kolejnych wyrazów tego osobliwego ciągu. Najpopularniejszy polega na tym, że każdy kolejny wyraz powstaje przez dopisanie do poprzedniego „negatywu” jego kopii (zera zastąpione są jedynkami, a jedynki zerami).
Wreszcie sposób, na który zwróciło uwagę kilku komentatorów, zaczynający się od ciągu, który jest dziesiętnym odpowiednikiem binarnego:
01, 0123, 01234567, 0123456789(10)(11)(12)(13)(14)(15),…
Aby otrzymać nasz ciąg binarny, wystarczy każdą liczbę (0, 1, 2, 3,…10, 11, 12…) w wyrazie zastąpić:
– zerem, jeśli liczba jedynek w jej zapisie dwójkowym jest parzysta,
– jedynką, jeśli liczba jedynek jest nieparzysta.

Bardzo trudno było dostrzec związek między ciągiem binarnym a dziesiętnym, ale umożliwiało to zastosowanie najprostszego sposobu uporania się z zadaniem. Wystarczyło liczbę 988 (odpowiada jej 2011 litera w ciągu piśnięć) zapisać w systemie dwójkowym i policzyć jedynki w zapisie.
Kto zaś odkrył sposób tworzenia ciągu przez dopisywanie negatywów kopii wyrazów, ten miał dłuższą drogę do celu. Oznaczając d(n) jako n-tą literę w wyrazie złożonym z 1024 znaków należało zauważyć, że d(1)=0, d(2)=1, d(4)=0, d(8)=1, d(16)=0, czyli ogólnie d(2^k )= k(mod2). Jeśli zaś n nie jest potęgą dwójki to d(n) = 1 – d(n-2^t), gdzie 2^t jest największą potęgą dwójki mniejszą od n.
Zatem d(989) = 1 – d(989-512) = 1 – d(477) = 1 – (1 – d(477-256) = d(221) = 1 – d(221-128) = 1 – d(93) = 1 – (1 – d(93-64) = d(29) = 1 – d(29-16) = 1 – d(13) = 1 – (1 – d(13-8)= d(5) = 1 – d(5-4)= 1 – d(1) = 1 – 0 = 1, czyli 2011 literą jest I.
Taki sposób, choć w bardziej zwięzłej formie, przedstawił w komentarzu m. in. uch.
Wiele innych ciekawych informacji dotyczących tego niezwykłego ciągu można znaleźć np. w angielskiej Wikipedii pod hasłem „Thue-Morse sequence„.

Kolejne zadanie wiąże się z całkiem innym ciągiem. Nie będzie to wprawdzie dobrze znany ciąg Fibonacciego, ale zacznę od niego:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,…
To wariant podstawowy, klasyczny, ale w zasadzie każdy ciąg utworzony na identycznej zasadzie – każdy następny wyraz (od trzeciego) jest sumą dwóch poprzednich – zaczynający się od dwóch dowolnych liczb, jest ciągiem Fibonacciego albo przynajmniej jego wariantem.
Czy istnieje ciąg Fibonacciego złożony wyłącznie z kwadratów liczb naturalnych? Nie i łatwo to udowodnić. W takim razie złagodzimy warunki:

Proszę znaleźć ciąg rosnący złożony z kwadratów liczb naturalnych, zaczynający się od jak najmniejszego kwadratu, w którym suma każdej pary kolejnych liczb jest kwadratem.

Wystarczy podać cztery początkowe wyrazy tego ciągu. Dodam, że w Encyklopedii ciągów liczbowych nie ma rozwiązania.

Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.