Bez cyfr

1 czerwca 2011
Marek Penszko

Każdy początkujący amator sudoku szybko zauważa, że im mniej cyfr jest na początku ujawnionych, tym trudniejsze zadanie. To wprawdzie nie reguła, ale zazwyczaj tak jest. Ciekawscy, zwłaszcza ci z matematycznym zacięciem,  z czasem zadają sobie pytanie: ile cyfr najmniej można ujawnić, aby zadanie miało jedno rozwiązanie? Japońscy miłośnicy sudoku już przed 20 laty zauważyli, że prawdopodobnie nie da się zejść poniżej siedemnastu. „Siedemnastki” pojawiały się jednak w prasie bardzo rzadko i raczej jako kurioza, ponieważ zwykle są rozrywkowe inaczej, czyli horrendalnie trudne. A jeśli w miarę łatwe, to także trudne, ale do ułożenia.

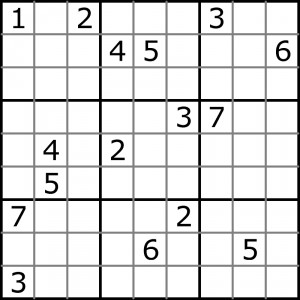
Gdy sudoku przed sześciu laty eksplodowało na świecie, 17-cyfrową granicę powtórnie odkryto na Zachodzie i próbowano ją przekroczyć. Pojawił się więc tzw. problem 16 cyfr, z którym programiści zmagali się różnymi metodami. Jedni szukali 16-cyfrowego diagramu wspólnymi siłami w ramach projektu przetwarzania rozproszonego BOINC, inni zbierali „siedemnastki” w nadziei, że uda się zejść oczko niżej, modyfikując którąś z nich. Za czołowego kolekcjonera uchodzi Gordon Royle, profesor matematyki z University of Western Australia w Perth, który w ciągu paru lat zgromadził blisko 50 tysięcy całkiem różnych siedemnastek z jednym rozwiązaniem. Na stronie pana profesora można je wszystkie pobrać, a przy okazji zapoznać się z niektórymi aspektami teoretycznymi zagadnienia. Zapewne najciekawszym efektem tej pasji jest szesnastka z dwoma rozwiązaniami:

Wbrew pozorom rozwiązywanie tej „bliźniaczki” nie jest trudne, choć jeżeli skorzystać z solvera Andrew Stuarta, to okaże się, że pokrętnych metod pod koniec zmagań nie sposób uniknąć. Mimo to nie stosując ich, ani też próbowania i błądzenia, dotarłem dość łatwo do celu, więc chyba solver przesadza.

Podobno to jedyna znana szesnastka z dwoma rozwiązaniami – z dokładnością do przekształceń diagramu (przestawienia rzędów, sektorów, liczb itp.), w wyniku których powstają inne szesnastki, ale nie całkiem inne, czyli jakby zmodyfikowane kopie.  Mam wątpliwości, bo przynajmniej jedna z innych znanych mi szesnastek wygląda na należącą do innej rodzinki, czyli całkiem inną niż powyższa. Ciężko to sprawdzić, aby mieć pewność, bo rodzinka liczy 1 218 998 108 160 diagramów. Ale próby trwają.

Problem 16 cyfr pozostaje otwarty. Nikt nie udowodnił, że 17 stanowi minimum. Tym niemniej wszyscy, którzy zgłębiali to zagadnienie, zgodnie twierdzą, iż pole poszukiwań zostało na tyle dokładnie „przeorane”, że znalezienie szesnastki byłoby sensacją graniczącą z cudem.

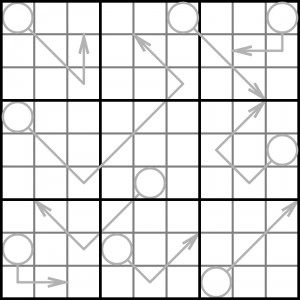
Natomiast nie jest cudem sudoku, w którym na początku w diagramie nie ma… ani jednej cyfry – nie ma też jakichkolwiek pomocniczych symboli literowych lub cyfrowych, jak np. w wariancie killer – a mimo to jest tylko jedno rozwiązanie. Chodzi oczywiście o niektóre odmiany klasycznej łamigłówki – takie, w których kluczem do rozwiązania są zależności między cyframi. Inaczej mówiąc, zamiast konkretnych cyfr można np. wskazać, w którym z dwóch sąsiednich pól powinna pojawić się większa albo oznaczyć jedną „niewidkę” jako sumę kilku innych. Moim zdaniem bezcyfrowe sudoku są najciekawsze w tym drugim przypadku, czyli w odmianie strzałkowej, o której wspominałem w dwóch poprzednich wpisach. Oto przykład takiego zadania, które na pierwszy rzut oka może się wydać nierozwiązywalne:

Przypominam zasady:
– reguła podstawowa: różne cyfry (od 1 do 9) powinny znaleźć się w każdym rzędzie, każdej kolumnie i w każdym sektorze 3×3 obwiedzionym grubą linią.
– reguła dodatkowa: każda cyfra w polu z kółkiem powinna być równa sumie cyfr w polach, które przecina strzałka wychodząca z kółka.

W rozwiązaniu wystarczy podać cztery cyfry w rogach diagramu.

Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.