Pierwsze strzałki
Podoba mi się strzałkowa odmiana sudoku, której przykład znalazł się w poprzednim wpisie. Zdecydowanie umieściłbym ją wśród dziesięciu najciekawszych sudokowych wariantów, przede wszystkim dlatego, że reguła dodatkowa jest formalnie prosta, a przy tym bardzo wzbogaca i „zakręca” logikę. Dzięki sumowaniu cyfr przybywa przesłanek, w których trzeba się połapać albo które trzeba po prostu dostrzec, by móc wyciągać wnioski. Tylko że zauważenie i połapanie się, to nie takie hop siup (chyba że jest się mistrzem), więc strzałkowe sudoku są zwykle dość trudne.
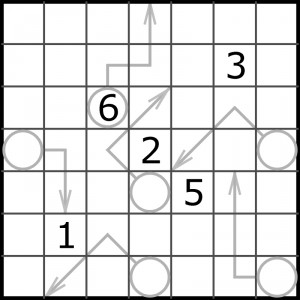
Jak większość sudokowych wariacji, także i ta ma japoński rodowód. Podstawowy pomysł pojawił się w nieco innym typie zadania, polegającym na wypełnianiu cyframi klasycznego kwadratu łacińskiego. Klucz do rozwiązania był dokładnie taki sam: niektóre cyfry zostały oznaczone jako sumy innych. Taka łamigłówka znalazła się w zestawie finałowym w mistrzostwach Japonii przed pięciu laty, a pomysł błyskawicznie przeskoczył do sudoku. Łaciński strzałkowy pierwowzór wyglądał tak:
Przypominam: cyfra w polu z kółkiem powinna być równa sumie cyfr w polach, które przecina strzałka wychodząca z kółka. A poza tym, jak zwykle w kwadratach łacińskich n x n, chodzi o wypełnienie pól cyframi od 1 do n, czyli w tym przypadku od 1 do 7, tak, aby w każdym rzędzie i w każdej kolumnie znalazły się różne cyfry.
Mimo stosunkowo małego diagramu zadanie nie jest łatwe. W rozwiązaniu wystarczy podać cztery cyfry w narożnych polach, ale wszystkich cyfr wymiana także mile jest widziana 🙂 .
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.

Komentarze
mniej niż 2 minuty:
3571462
2614735
4763251
5342176
6237514
7125643
1456327
3571462
2614735
4763251
5342176
6237514
7125643
1456327
Witam,
ja tu widzę dwa rozwiązania. Tylko nie wiem, czy coś mi umknęło, czy faktycznie są dwa rozwiązania. Podaję oba:
2751364
5614732
7563241
6432175
4276513
3127456
1345627
2751463
5614732
7563241
6432175
3276514
4127356
1345627
A więc w rogach mogą być 2317 bądź 2317.
Pozdrawiam.
Mini-konkurs: znajdź błąd
mp
3571462
2614735
4763251
5342176
6237514
7125643
1456327
W mojej ocenie – b. łatwe 🙂 Łatwiejsze niż to poprzednie zadanie. Pozdrawiam 🙂
Rząd drugi z prawej, na dole: 2+5+1 nie równa się 7. Pozdrawiam 🙂
3 2
1 7
zadanie lekkie, łatwe i przyjemne. dla najlepszych pewnie na niecałą minutkę:)
takich przyjemnych zadań jak najwięcej życzę finalistom Mistrzostw Polski w Łamigłowkach oraz finalistom sudokowiczom w sobotę w Warszawie
pozdrawiam
pafcio
Cyfry w rogach: gornych – 3, 2; dolnych – 1, 7.
Dosc proste.
a
3217
Prawdę mówiąc bez błędnego rozwiązania Agnieszki nie udało mi się rozwiązać. Nie mogłem wpaść na to, że na „ścieżce” wychodzącej z szóstki mogą być dwie jedynki.
Pozdrawiam
Bardzo fajne zadanie, podpasowało mi wybornie:)
3571462
2614735
4763251
5342176
6237514
7125643
1456327
3571462
2614735
4763251
5342176
6237514
7125643
1456327
20 minut ! ! ! !