Kulaj się
Tkwię ostatnio po uszy w matematyce bilardu. Wnioskując z rekwizytów i zasad temat wydaje się prosty, bo bilard matematyczny to tylko jedna kula na stole bez łuz, odbijająca się od band zgodnie z zasadą: kąt odbicia równy jest kątowi padania. W dodatku wszelki opór pomijamy, czyli np. snookerowe sztuczki związane z rotacją, w rodzaju krzywoliniowego toru, są wykluczone. Pchnięta kula toczy się w nieskończoność, chyba że trafi do rogu. Wtedy staje, bo „nie wie” co robić dalej. Tory, które pobłądzą w załamania bandy, nie są w bilardowej matematyce w ogóle analizowane.
Prostota tematu jest pozorna. Przeciwnie, jest on zaskakująco ciekawy i zawiły, ponieważ stoły mogą mieć dowolny kształt, nie wyłączając krzywoliniowych band i trzeciego wymiaru, czyli bilardu w bryłach. W tym ostatnim przypadku praktyczna zabawa jest niebezpieczna, bo kule świszczą koło uszu.
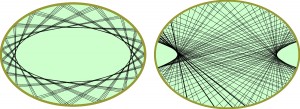
Bila poruszająca się na eliptycznym stole po niecyklicznym torze (na cykliczny są małe szanse) i znacząca ślad w postaci cienkiej czarnej linii, pozostawi „czystą” mniejszą elipsę lub dwa obszary ograniczone fragmentem hiperboli – zależnie od tego, gdzie przetnie wielką oś, ruszając w drogę.
Przyjemnie obserwować na ekranie monitora, jak stopniowo wyłaniają się te białe obszary, ale znacznie bardziej widowiskowe są symulacje komputerowe ruchu kuli na stołach o wyrafinowanych kształtach. Kto nie widział obrazków, jakie maluje bila śladem swojej wędrówki na stole w kształcie górnej lub dolnej płyty skrzypiec, ten ma czego żałować.
Nawet najprostszy wieloboczny, czyli trójkątny stół bywa bardzo zagadkowy. Jeśli jest trójkątem równobocznym, to wyznaczenie na nim 3-etapowego toru cyklicznego jest trywialne.
Gdy jednak kąty trójkąta się zmieniają, zadanie przestaje być takie proste, a narysowanie cyklu obejmującego trzy etapy może być niemożliwe.
Gwoli ścisłości: cykl jest n-etapowy, jeśli na trasie między dwoma kolejnymi zaliczeniami punktu startowego kula (n-1)-krotnie zmienia kierunek.
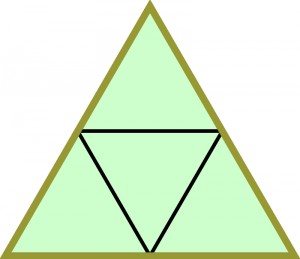
Pytanie (niełatwe, bo trochę podstępne 😉 ): jaki powinien być trójkąt, aby w jego wnętrzu kula mogła poruszać się po cyklicznym torze 4-etapowym?
Kto odpowie w dwóch słowach?
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.

Komentarze
Dowolny trójkąt.
Nie za bardzo rozumiem liczbę zmiany kierunków i liczbę etapów… coś mi tu nie gra. W załączonym obrazku widzę 3 zmiany kierunku i trzy etapy w opisie, zaś poniżej napisał Pan, że zmian kierunku jest o jeden mniej niż liczba etapów… poproszę jaśniej.
Liczę zmiany kierunków w trakcie jednego cyklu – n-ta zmiana następuje dopiero w momencie rozpoczęcia następnego cyklu.
mp
Odpowiem jednym słowem 🙂 : prostokątny
A jednak dwoma 🙁 : prostokątny, równoramienny
Równoramienny prostokątny
Prostokątny równoramienny.
Trojkat powinien byc prostokatny i rownoramienny.
a
Trójkąt powinien mieć co najmniej jeden bok wypukły. Można wtedy zrobić drogę na przykład o kształcie kwadratu. Bierzemy trójkąt prostokątny, gdzie jego przeciwprostokątną jest wycinek okręgu o odpowiednim promieniu.
Ja stawiam na trójkąt prostokątny, w którym oba kątry ostre wynoszą 45 stopni.
Wybijam bilę z jednej przyrostokątnej pod kątem prostym. Bila odbija się od przeciwprostokątnej, potem od drugiej przyprostokątnej (pod kątem prostym!) i TĄ SAMĄ drogą powraca do puntu startowego.
W efekcie – zgodnie z definicją – cykl jest 4 etapowy, chiciaż tor wygląda jak dwuetapowy 🙂
Odpowiedzi „prostokątny, równoramienny” są oczywiście poprawne, ale niepełne. Zapewne dlatego, że przesadziłem z podstępnością, prosząc o podanie odpowiedzi w dwóch słowach. Wystarczy jedno: „równoramienny”. Kula pokonuje 4-etapowy cykl tak, jak to opisał San Rokiz, niezależnie od wielkości kąta między ramionami: startuje z ramienia pod kątem prostym z takiego punktu, by trafić w środek podstawy i wraca po odbiciu się od drugiego ramienia i dwukrotnie od podstawy. Cykl jest 4 etapowy – w tą i z powrotem po tej samej 2-odcinkowej trasie.
Szczerze mówiąc, prośba o odpowiedź w dwóch słowach wynikła z mojego trywialnego błędu. Nie wiem dlaczego uznałem, że trójkąt nie może być ostrokątny – wtedy odpowiedź brzmiałaby trochę nietypowo: „równoramienny, nieostrokątny”.
mp
Witam
Panie Marku. Kula nie musi trafiać w środek podstawy. Ważne jest tylko aby startowała pod kątem prostym z dowolnego ramienia w kierunku podstawy.
Pozdrawiam
I zawsze będzie cykl? I 4-etapowy?
mp
Zawsze o ile będziemy trafiać w podstawę. Przy przesuwaniu równoległym (bo ciągle pod kątem prostym do ramion) zmieniać będą się długości poszczególnych odcinków ale nie kąty odbicia.
Pozdrawiam
A jeśli kąt trójkąta przy podstawie będzie wynosił jeden stopień (skrajny przypadek) i kula (punkt) wystartuje z ramienia tuż obok wierzchołka tego kąta?
mp
Każdy równoramienny!
Panie Marku!
Nie musi trafiać w środek podstawy. W każdym trójkącie równoramiennym jest nieskończenie wiele takich cykli.
Zgoda, ale czy może trafiać w dowolny punkt podstawy?
mp
W dowolny punkt podstawy trafi tylko wtedy, gdy nie będzie to trójkąt rozwartokątny.
jazz
PS
Jakiego programu użył Pan tworząc na monitorze obrazy takie jak na rys. Kul_1? Też chciałbym to zobaczyć.
Pozdrawiam.
Mathematica 3.0 – stareńka wersja, ale są znacznie nowsze. Za friko może uda się tu http://demonstrations.wolfram.com/ReflectionsInAnEllipticalRegion/
Próbowałem pobrać program, ale program antywirusowy zaczął wyświetlać groźne komunikaty i wystraszyłem się 🙂
mp
Jeśli przyjmiemy model punktowej (bezwymiarowej) kuli to może trafiać w dowolny punkt podstawy niebędący wierzchołkiem trókąta. W przypadku rzeczywistego modelu posiadającego jakieś wymiary wybór punktu trafienia w podstawę będzie ograniczony wymiarami kuli.