Przekładanka

19 lutego 2011
Marek Penszko

Cztery jednakowe kwadraty można połączyć – bok do boku – na pięć różnych sposobów. Utworzony w ten sposób zestaw pięciu figur zwany jest tetrominem. Te pięć klocków (kamieni) zna każdy, kto miał do czynienia ze starą, ale wciąż jarą grą tetris. Pojawiają się one także w wielu łamigłówkach. Oto jedna z nich, będąca równocześnie treningiem wyobraźni.

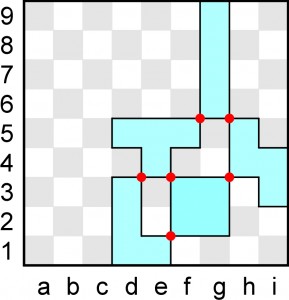
Piątka tetromino leży na szachownicy 9×9 tak, że kamienie stykają się tylko rogami w sześciu punktach. Proszę zmienić położenie tylko dwóch kamieni tak, aby wszystkie nadal stykały się tylko rogami, ale w siedmiu punktach. Przekładane kamienie wolno obracać i odwracać na drugą stronę. Żaden z nich nie może jednak po przemieszczeniu wystawać poza planszę.

Warto spróbować uporać się z przekładanką bez korzystania z jakichkolwiek rekwizytów, czyli wyłącznie w głowie. Jako rozwiązanie można podać współrzędne pól zajętych przez przełożone kamienie.
Pytanie dodatkowe: ile rozwiązań ma to zadanie?

Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.