Sudoku Eulera

28 listopada 2010
Marek Penszko

Gdy przed niespełna 6 laty zaczęła się epidemia sudoku, częściową odpowiedzialnością za ten kataklizm – gwoli dodania mu splendoru – obarczono XVIII-wiecznego matematyka szwajcarskiego Leonharda Eulera. Chodziło o to, że ów Bogu ducha winny uczony zajmował się jakoby tzw. kwadratami łacińskimi, a sudoku właśnie takim kwadratem jest, choć nieco zakręconym.
Wplątanie Eulera w tę sprawę było przynajmniej przesadą, jeśli nie nieporozumieniem, bowiem miał on ze znanymi od wieków kwadratami łacińskimi tylko tyle wspólnego, że nadał im nazwę, która się przyjęła (wcześniej podczepiano je pod kwadraty magiczne). Natomiast wnikliwiej interesował się pod koniec życia podobnymi obiektami własnego pomysłu, ale jednak wyraźnie odbiegającymi od sudoku – kwadratami, które nazwał grecko-łacińskimi (nazwa stąd, że symbolami wpisywanymi w kratki były litery alfabetu łacińskiego i greckiego).

W kwadracie łacińskim n x n, podobnie jak w sudoku, w każdej kratce tkwi jeden z n różnych symboli należących do zbioru A tak, że żaden symbol nie powtarza się w żadnym wierszu ani kolumnie.
Natomiast kwadrat grecko-łaciński n x n, to jakby kwadrat łaciński typu „dwa w jednym”. W każdej kratce znajduje się para symboli, z których jeden należy do zbioru A (a1, a2, a3…, an), drugi do zbioru B (b1, b2, b3…, bn). Układ symboli a tworzy kwadrat łaciński i układ symboli b także tworzy kwadrat łaciński, ale – i to jest najistotniejsze – taka sama para symboli nigdzie się nie powtarza.
Eulerowi można by więc przypisać tylko taką odmianę sudoku, która polegałaby na wpisaniu w diagram 9×9 wszystkich liczb dwucyfrowych, nie zawierających zera, w taki sposób, aby cyfry oznaczające jednostki tworzyły jedno zwykłe sudoku, a oznaczające dziesiątki – drugie. Pojawiła się nawet taka odmiana, ale ponieważ jej rozwiązywanie było cierpiętnicze, więc szybko trafiła do lamusa osobliwości.

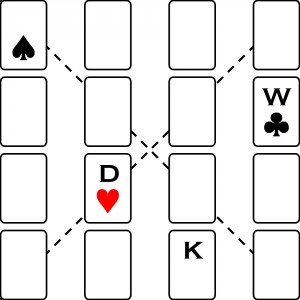
Znacznie prostsze, adresowane raczej do początkujących główkołamaczy, są znane od dawna zadania z mniejszymi kwadratami grecko-łacińskimi i z wykorzystaniem niejako naturalnego surowca, nadającego się do ich układania, czyli kart do gry. Każda karta jest gotową parą symboli, z których jeden należy do zbioru wartości (rang), a drugi do zbioru kolorów. Ponieważ kolory są cztery, więc zabawa ogranicza się do kwadratów 4×4.
Poniżej taki kwadratowy układ tworzą wyjęte z talii wszystkie figury (4 asy, 4 króle, 4 damy, 4 walety):

W każdym rzędzie i w każdej kolumnie są różne figury i różne kolory, a na przekątnych różne figury (kolory niekoniecznie różne).
Niektóre symbole rang i kolorów ujawniono. Proszę ujawnić pozostałe.

Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.